仅作个人用途。CS50AI 课程的笔记。

0. Search

什么能够制造AI：

  1. 搜索：寻找问题的解决方案
  2. 知识：展示信息和相关知识
  3. 不确定性：使用概率来解决不确定的事件
  4. 优化：不单是找到解决问题的正确方案，而是找到更好更棒的解决方案
  5. 学习：基于对数据和经验的获取而提高性能
  6. 神经网络：一种受人脑启发的程序结构，能够有效地执行任务
  7. 语言：处理由人类产生和理解的自然语言

搜索

搜索问题设计了一个代理，它：

  • 被赋予一个初始状态
  • 被赋予一个目标状态
  • 返回一个如何从前者到后者的解决方案

解决搜索问题

解决方案是从初始状态到目标状态的一连串行动。

而最佳解决方案，是一个在所有解决方案中具有最低路径成本的解决方案。

在搜索过程中，数据通常被存储在一个节点（node）中。节点是一个数据结构，包含：

  • 一个状态

  • 父节点

  • 应用于父节点状态的行动，以达到当前节点的目的

  • 从初始状态到这个节点的路径成本

节点包含的信息对搜索算法的目的很有用。不过节点仅持有信息。为了实际搜索，我们使用前沿（frontier），即管理节点的机制。

前沿开始时包含一个初始状态和一个空的已探索集合，然后重复直到达到一个解决方案：

  1. 如果前沿是空的：

    • 停止。这个问题没有解决方案

  2. 从前沿中移除一个节点，该节点会被考虑

  3. 如果节点持有目标状态：

    • 返回解决方案。停止

    否则：

    1. 扩展节点（找到所有可以从这个节点到达的新节点）
    2. 将产生的节点添加到前沿
    3. 将当前节点添加到已探索集合中

上述没有提到哪个节点应该被移除。这个选择对解决方案的质量和实现的速度都有影响。有多种方法可以解决哪些节点应该被首先考虑：

  1. 堆栈/深度优先搜索（stack/depth-first search）
  • 在尝试另一个方向之前会穷尽每一个方向
  • 前沿被作为一个堆栈数据结构来管理
  • “后进先出”
  • 当节点被添加到前沿之后，第一个要移除和考虑的节点是最后被添加的节点
  • 在第一个方向上尽可能地深入，而把所有其他方向留给以后

例子：你在寻找钥匙

  1. 选择从裤子开始搜索
  2. 先翻遍每一个口袋
  3. 当裤子的每个口袋里都找完了，再停止对裤子的搜索
  4. 搜索其他地方

优点：

  • 在最好的情况下，速度最快

缺点：

  • 找到的解决方案有可能并不是最优的
  • 在最坏的情况下，可能在找到解决方案之前就探索了所有可能的路径，导致花费了更长的时间
1
2
3
4
5
6
7
8
9
10
def remove(self):
    if self.empty():
        # 如果前沿是空的，终止搜索
        raise Exception("空前沿")
    else:
        # 保存最新添加的节点
        node = self.frontier[-1]
        # 从前沿里移除最新添加的节点
        self.frontier = self.frontier[:-1]
        return node
  1. 队列/广度优先搜索（queue/breadth-first search）

  • 同时遵循多个方向

  • 在每个可能的方向上走一步，然后在每个方向上走第二步

  • 前沿被作为一个队列数据结构来管理

  • “先进先出”

  • 所有的新节点都是排队增加的

  • 节点被考虑的依据是哪一个先被添加

例子：你又在找钥匙

  1. 从裤子开始搜索
  2. 从裤子右边口袋里寻找
  3. 在抽屉里看一看
  4. 在桌子上看
  5. 用尽了所有的位置之后，回到裤子，寻找下一个口袋

优点：

  • 保证能找到最优解

缺点：

  • 运行的时间比最小时间长
  • 在最坏的情况下，这个算法需要尽可能长的时间来运行
1
2
3
4
5
6
7
8
9
10
def remove(self):
    if self.empty():
        # 如果前沿为空，终止搜索
        raise Exception('空前沿')
    else:
        # 保存第一个被添加的节点
        node = self.frontier[0]
        # 从前沿中移除第一个节点
        self.frontier = self.frontier[1:]
        return node

  1. 贪婪的最佳优先搜索（greedy best-first search）

    广度优先和深度优先都是无信息的搜索算法。这些算法不利用任何它们没有通过自己的探索而获得的关于问题的知识。然而，关于问题的一些知识实际上是可用且常用的。

    • 扩展了最接近目标的节点
    • 该行为由启发式函数（heuristic function）决定
    • 函数估计下一个节点离目标有多近，但可能是错误的

  2. A*搜索（A* search）

    作为贪婪的最佳优先算法的发展，A*搜索不仅考虑了启发式函数 h(n)h(n)，还考虑了直到当前位置的累计成本 g(n)g(n)。结合这两个值，该算法确定解决方案的成本更精准，还会优化其在路上的选择。

    该算法会一直跟踪 到现在位置的路径成本 + 到目标的估计成本。一旦超过之前某个选项的估计成本，该算法就会抛弃当前的路径，回到之前的选项，从而避免自己走一条被 h(n)h(n) 错误地标记为最佳、实际为漫长且低效的路径。

    这个算法也依赖着启发式。某些情况下，效率要比贪婪的最佳优先搜索低，甚至低于无信息的算法。为了使A*搜索成为最优，启发式函数应该是：

    • 可接受的/永远不会高估真实成本

    • 一致性

    • h(n)<=h(n′)+ch(n) <= h(n') + c

  3. 对抗性搜索（adversarial search）

    该搜索中，算法面临着一个试图实现相反目标的对手。例如井字棋。

    1. 极小化极大（minimax）

      对抗性搜索中的一种算法：

      • 将一方的获胜条件表示为-1，另一方的获胜条件为+1
      • 进一步的行动将由这些条件驱动

      井字棋AI：

      • s₀s₀ 代表初始状态（一个空的3x3棋盘）
      • Players(s)：参数s是一个状态；返回哪个玩家的回合（X或者O）
      • Actions(s)：参数s是一个状态；返回当前状态所有有效的移动（棋盘上哪些格子是空闲的）
      • Results(s,a)：参数s和a分别是一个状态和一个行动；返回一个全新的状态（在状态s上执行行动a后的棋盘）
      • Terminal(s)：参数s是一个状态；检查是否是棋盘中最后一次行动（是否有人胜出或平局）；如果游戏结束返回True，反之返回False
      • Utility(s)：参数s是一个临终状态；返回该状态的效用值：-1、0、1

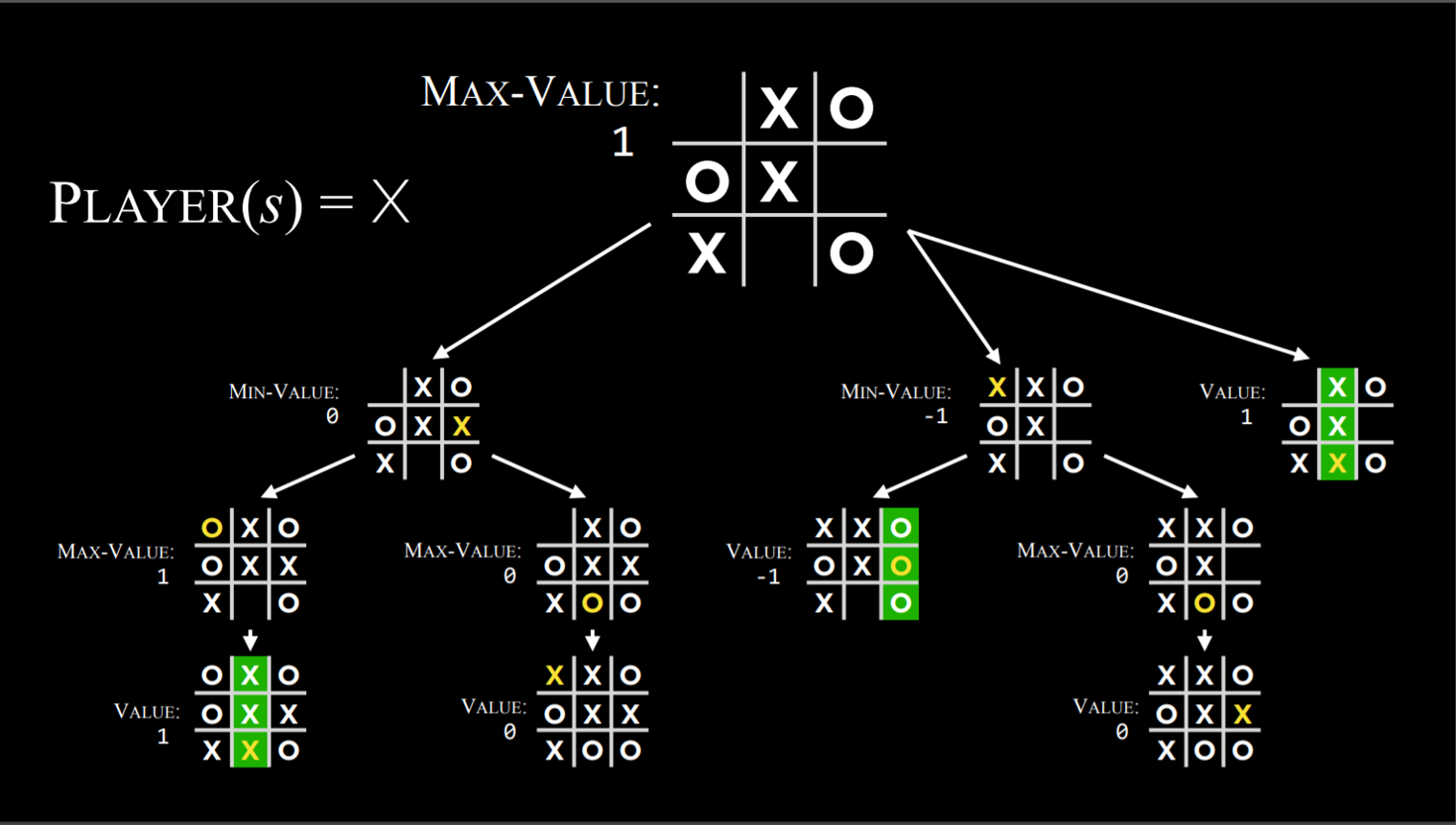
      Minimax in Tic Tac Toe

      1. 根据状态（本回合轮到谁），该算法可以知道当前的玩家在进行优化游戏时是否会选择导致了一个较低/较高数值的状态的行动
      2. 在最小化和最大化之间交替进行
      3. 为每个可能的行动所导致的状态创造值
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      Function Max-Value(state):
      v = -∞
      if Terminal(state):
      	return Utility(state)
      for action in Actions(state):
      	v = Max(v,Min-Value(Result(state,action)))
      	return v

            Function Min-Value(state):
                v = ∞
                if Terminal(state):
                    return Utility(state)
                for action in Actions(state):
                    v = Min(v,Max-Value(Result(state,action)))
                    return v

    2. Alpha-beta剪枝（alpha-beta pruning）

    作为优化极小化极大的一种方式，Alpha-beta剪枝跳过了一些明显不利的递归计算。

    在确定了一个行动的值后，如果有初步证据表明之后的行动可以使对手得到比已经确定的行动更好的分数，那么就没有必要进一步研究这个行动，因为它将决定性地比之前确定的行动更不利。

    例子：

    一个最大化的棋手知道：在下一步，最小化的棋手将试图达到最低分数。

    假设最大化的棋手有三个可能的行动，第一个行动的值为4。为此，如果当前棋手实施了该行动，棋手会生成最小化者的行动值，因为他知道最小化者会选择最低的行动。

    然而，在完成对最小化者的所有可能行动的计算之前，棋手看到其中一个选项的值为3。这意味着对于最小化者来说，没有理由继续探索其他可能的行动。尚未取值的行动的值并不重要，无论是10还是-10。

    如果值是10，最小化者就会选择最低的选项，也就是3，这已经比预先确定的4更糟糕。因此，此时计算最小化者的额外可能行动与最大化者无关，因为最大化者已经有一个明确的更好的选择，即4。

    1. 深度有限的极小化极大（depth-limited minimax）

    井字棋一共有255168个可能，而国际象棋有 1029010^{290} 个可能。到目前为止，极小化极大算法要求生成从某一点到目标条件的所有假设。虽然计算所有的井字棋游戏假设对现代计算机来说并不困难，但如果在国际象棋里呢？

    深度限制的极小化极大在停止前只考虑先定义的棋步数，而不去考虑临终状态。然而这并不允许为每个行动获取一个精确的数值，因为假想游戏的终点还未达到。

    为了处理这个问题，深度有限的极小化极大依赖于一个评估函数，该函数估计了从给定状态开始的游戏的预期效用，或者换句话说，为状态赋值。

    例子：

    在国际象棋中，一个效用函数将棋盘的当前配置作为输入，试图评估其预期效用（基于每个玩家拥有的棋子和它们在棋盘上的位置），然后返回一个正值或负值，代表棋盘对一个玩家与另一个玩家的有利程度。

    这些值可以用来决定正确的行动。评估函数越好，依赖它的极小化极大算法就越好。

作业Degrees

根据 Six Degrees of Kevin Bacon 游戏，好莱坞电影界的任何人都可以在6个步骤内与 Kevin Bacon 联系起来，其中每个步骤都包括找到两个演员都出演的电影。

问题：通过选择一连串的电影，找到任何两个演员之间的最短路径。

例子：Jennifer Lawrence 和 Tom Hanks 的最短路径为2。

  1. Jennifer Lawrence 和 Kevin Bacon 都出演了《X-Men: First Class》
  2. Kevin Bacon 和 Tom Hanks 都出演了《Apollo 13》

分发代码

  1. large目录下的csv数据文件

  2. small目录下的csv数据文件（用于测试）：
    在small目录下的people.csv中，能看到每个人都有一个独特的id、他们的名字和生日；在movies.csv中，每个电影都有一个独特的id、它们的标题和发布的年份；在stars.csv中，每一行都是一组人的id和电影的id。

    例子：人的id为102，电影的id为104257。这代表了 Kevin Bacon 出演过《A Few Good Men》。

  3. degrees.py。在最上方一些数据结构被定义（names、people、movies），这些数据结构将保存从CSV文件中的信息。

    • names字典，将名字映射到一组对应的id（可能有多个演员有相同的名字）
    • people字典，将人id映射到另外一个字典（存有名字、出生年份、主演的所有电影的集合）
    • movies字典，将电影id映射到另外一个字典（存有标题、发行年份、所有出演演员的id）

    文件已经事先定义了一个函数load_data()，它从CSV文件里加载数据，并存在上述这些数据结构中。

    主函数main()首先将数据加载到内存中（加载数据的目录需要通过命令行参数指定）。之后函数会提示用户输入两个名字，另一个函数person_id_for_name()会检索这个名字并返回id（如果有多个演员叫这个名字，就会提示用户找出正确的id）。然后主函数会调用shortest_path()来计算这两个人之间的最短路径，并打印出这个路径。

    然而，shortest_path()要你来写。

目标

完成shortest_path()的实现，使其返回源id到目标id的最短路径

  1. 假设有一条从源id到目标id的路径，你的函数应该返回一个列表，每个元素是一个元组：(movie_id, person_id)
  2. 如果shortest_path()返回了[(1, 2), (3, 4)]，那就意味着源id和人2一起出演了电影1，人2在电影3中和人4出演，而人4是目标
  3. 如果从源id到目标id之间有多条最小长度的路径，你的函数可以返回其中的任何一条
  4. 如果两个演员之间没有可能的路径，你的函数应该返回None
  5. 你可以调用neighbors_for_person()，该函数接收一个人的id作为参数，并返回装有(movie_id, person_id)元组的集合（这些人都和提供的人出演过电影）

作业Tic-Tac-Toe

分发代码

项目中有两个主要文件：runner.py 和 tictactoe.py，后者包含了所有玩游戏、做出最佳动作的逻辑，而前者包含了所有运行游戏的代码。

tictactoe.py 定义了三个变量：X、O、EMPTY，代表了棋盘上可能出现的移动。

函数initial_state()返回棋盘的起始状态。将棋盘表示为三个列表以代表三行，其中每个内部列表都包含了我们刚定义的变量的值。

目标

完成player()、actions()、result()、winner()、terminal()、utility()，和minimax()这些函数。

  1. player()接受棋盘状态作为输入，然后返回当前回合属于哪个棋手

    • 棋盘初始化时，棋手X先手下棋

  2. action()返回一个装有在当前棋盘上可以采取的所有行动的集合

    • 每个行动是一个元组(i, j)，其中i对应行，j对应一行中的单元格
    • 可以采取的行动代表的是在棋盘上任何尚未有X或者O的单元格

  3. result()接受一个棋盘和一个行动作为输入，然后返回一个新的棋盘状态

    • 如果动作并不有效，程序应该引发一个异常

  4. winner()接受一个棋盘作为输入。如果已经有人胜出，返回赢家

    • 假设棋手X赢了，就返回X

    • 胜利目标：在水平、垂直或对角线上连续走了三步

    • 如果平手，则返回None

  5. terminal()接受一个棋盘作为输入，然后返回一个布尔值，表示游戏是否结束

  6. utility()接受一个结束了的棋盘作为输入，并输出该棋盘的效用

    • 如果棋手X胜利，效用为1；如果棋手O胜利，效用为-1；如果平局，效用为0
    • 只有在terminal(board)为True时才会调用该函数

  7. minimax()接受一个棋盘作为输入，并返回棋手在棋盘上的最佳行动

    • 返回的应该是最优行动(i, j)
    • 如果多个行动是最优的，那么任意一个行动都可以被返回
    • 如果棋盘是结束了的棋盘，返回None

1. Knowledge

人类根据现有的知识进行推理并得出结论。人工智能也可以从知识里得出结论。

什么是”基于知识进行推理以得出结论“？

考虑以下这些句子：

  1. 如果没有下雨的话，哈利今天就会去拜访海格了
  2. 哈利今天拜访了海格或邓布利多，但没有同时拜访
  3. 哈利今天拜访了邓布利多

根据这三个句子，我们可以回答”今天下雨了吗？“这个问题，尽管没有一个单独的句子告诉我们关于今天是否下雨的信息。我们可以这样做：看句子3，得知哈利拜访了邓布利多；看句子2，得知哈利拜访了海格或邓布利多。因此我们可以得出结论：

  1. 哈利没有拜访海格

现在再去看句子1，我们明白，如果没有下雨，哈利就会去拜访海格。了解了句子4后，我们可以得出结论：

  1. 今天下雨了

逻辑，我们使用了逻辑来得出结论。人工智能该如何使用逻辑在现有信息的基础上得出新的结论？

句子是人工智能存储知识并使用它来推断新信息的方式。

命题逻辑

命题逻辑以命题为基础，即可以是真的、也可以是假的、关于世界的陈述。例如上述的句子1~5。

  1. 命题符号

    • 最常见的是字母（P、Q、R），用于表示一个命题

  2. 逻辑连接词

  • 连接命题符号的逻辑符号，以便以更复杂的方式对世界进行推理

  1. ¬，”不“符号，用于反转命题的真值。例如P是”正在下雨“，¬P就是”没有下雨“

  2. ^，”和“符号，用于连接两个不同的命题

  3. ∨，“或”符号，只要其中一边是真，那就是真

1. 排他性“或”：如果`P^Q`为真，那`P∨Q`就是假；排他性语句只要求其中一个参数为真
2. 包容性“或”：只要`P`、`Q`、`P^Q`为真，那就是真

我们会更倾向于使用包容性“或”。

> 更多的例子：
>
> - 包容性“或”：为了吃甜点，你必须清理你的房间或者修剪草坪
> 	- 如果你清理了房间，还修剪了草坪，你仍然会吃到甜点
> - 排他性“或”：甜点的话，你可以吃饼干或者吃冰淇淋
> 	- 你不能同时吃到饼干和冰淇淋
> 	- 排他性“或”通常被简称为XOR，符号是⊕

  1. →，“暗示”符号，表示“如果P那么Q”的结构。例如P是“正在下雨”，Q是“我在室内”，那么p→Q意味着“如果正在下雨，那么我在室内”。这个案例中，P被称为前项（antecedent），Q被称为后项（consequent）

    • 如果前项为真，后项为真，那么整个暗示就为真
    • 如果前项为真，后向为假，那么整个暗示就为假
    • 然而，当前项为假，后项为真时，暗示总是真的

  2. ↔，“双条件”符号，或“如果&只有当”。P↔Q相当于P→Q和Q→P。引用上述的例子，P↔Q就是“如果正在下雨，那么我在室内”和“如果我在室内，那么正在下雨”

模型

模型是对每个命题的真值的分配，而命题是关于世界的陈述，可以是真也可以是假。然而，关于世界的知识就体现在这些命题的真值中。模型是提供关于世界的信息的真值分配。

例如，P是“正在下雨”，Q是“今天是周二”，一个模型可以是以下的真值赋值：{P=True, Q=False}。这个模型意味着正在下雨，但今天不是周二。在这种情况下还有更多可能的模型，例如{P=True, Q=True}，也就是现在既下雨，也是周二。

事实上，可能的模型的数量是命题的数量的两倍。如果我们有两个命题，那就有 222^2 个可能的模型。

知识库

知识库是一组被基于知识的代理所知道的句子，也就是人工智能以命题逻辑句子的形式提供的关于世界的知识，可以用来对世界进行额外的推断。

蕴涵（⊨）

如果α⊨β，那么在任何α为真的世界中，β也是真的。

  • 例如α是“这是一月中的一个周二”，β是“这是一个周二”，然后α⊨β。那么我们能知道这是一个在一月内的周二，并且这是一个周二
  • 蕴含和暗示不同。暗示是两个命题间的逻辑连接词，而蕴含是一种关系，意味着如果α中所有的信息都是真，那么β中所有的信息也都是真

推理

推理是指从旧的句子中推导出新的句子的过程。

例如上述的哈利波特例子中，句子4~5是句子1~3中推断出来的。

有多种方法可以在现有知识的基础上推断出新的知识。首先，我们将考虑模型检查算法（Model Checking algorithm）。

  • 为了确定KB⊨α（换言之，回答问题“我们能否根据我们的知识库得出α为真的结论”）：

    • 列举所有可能的模型
    • 如果每个模型中KB为真，那么α也都是真的，因此KB⊨α

  • 再考虑这个例子：

    • P是“今天是星期二”，Q是“现在在下雨”，R是“哈利要去跑步”

    • KB：(P^¬Q) → R，用话说就是：P和¬Q暗示了R。P是真，Q是假，那么R是真还是假？KB是否⊨R？

    • 先列举出所有可能的模型

      命题 值
      P
      Q
      R      		 false
      false
      false
      P
      Q
      R      		 false
      false
      true
      P
      Q
      R      		 false
      true
      false
      P
      Q
      R      		 false
      true
      true
      P
      Q
      R      		 true
      false
      false
      P
      Q
      R      		 true
      false
      true
      P
      Q
      R      		 true
      true
      false
      P
      Q
      R      		 true
      true
      true

    • 通过每一个模型，检查它在我们的知识库中是否为真

    • 首先，我们知道P为真，因此所有P为假的模型里，KB都为假。同样地，我们知道Q为假，因此所有Q为真的模型里，KB都为假。最终我们只剩下两个模型，P都是真且Q都是假。我们知道R是真，因此最后R为假的模型中，KB自然也是假

    • 再来看看我们的表，我们只有一个KB为真的模型。根据蕴含的含义，得出KB⊨R

    • 这些知识和逻辑可以被这样写：

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      from logic import *

      # 创建新的类，每个类都有一个名字或符号，代表命题
      rain = Symbol("rain")  # 在下雨
      hagrid = Symbol("hagrid")  # 哈利见海格
      dumbledore = Symbol("dumbledore")  # 哈利见邓布利多

      # 将句子保存进知识库
      # 先使用“和”逻辑，因为每个命题都代表了我们已知为真的知识
      knowledge = And( 
      	Implication(Not(rain), hagrid),  # ¬(在下雨)→(哈利见海格)
          Or(hagrid, dumbledore),  # (哈利见海格)∨(哈利见邓布利多)
          Not(And(hagrid, dumbledore)),  # ¬(哈利见海格^哈利见邓布利多)，但没有见两人
          dumbledore  # 哈利见邓布利多（事实）
      )

    • 要运行模型检查算法，我们需要这些信息：

      • 知识库，用于推理
      • 一个查询，或我们感兴趣的命题是否被KB所包含
      • 一个装有所有被使用的符号（或原子命题）的列表（也就是我们案例中的rain、hagrid、dumbledore）
      • 模型
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      def check_all(knowledge, query, symbols, model):
          # 如果模型有分配给每个符号
          # 逻辑：从一个符号列表开始。函数递归时，每次的调用都会从列表中删除一个符号，并从中生成模型。当符号列表为空时，我们知道我们已经完成了对符号的每一个可能的真值分配的模型生成
          if not symbols:
              # 如果在模型中的KB为真，查询也就是真
              if knowledge.evaluate(model):
                  return query.evaluate(model)
              return True
          
          else:
              # 选择剩余的未使用符号的其中一个
              remaining = symbols.copy()
              p = remaining.pop()
              
              # 创建一个符号为真的模型
              model_true = model.copy()
              model_true[p] = True
              
              # 创建一个符号为假的模型
              model_false = model.copy()
              model_false[p] = False
              
              # 确保两个模型中都有蕴含关系
              return(
                  check_all(knowledge, query, 
                            remaining, model_true) 
                  and 
                  check_all(knowledge, query, 
                            remaining, model_false)
              )

    • 我们只对KB为真的模型感兴趣。如果KB为假，那么这个模型就和我们的案例无关

      例子：

      • P为“哈利扮演seeker”、Q为“奥利弗扮演keeper”，R为“格兰芬多获胜”
      • KB规定P Q (P ^ Q) → R
        • 也就是P为真，Q为真，那么R也为真
      • 想象一个模型，哈利扮演的是beater而非seeker，也就是P为假。这种情况下我们并不关心格兰芬多是否胜利（即R是否为真）。因为我们只对P和Q为真的模型感兴趣

    • 此外，check_all()的工作方式是递归的。也就是说它会选择一个符号，创建两个模型，其中一个符号为真，另一个符号为假，然后再次调用自己，现在有两个模型因这个符号的真值分配而不同。这个函数会一直这样做，直到所有的符号都在模型中被分配了真值、让列表中的符号为空。一旦列表为空，函数会在每个实例中检查模型中的KB是否为真。如果为真，函数就会检查查询是否为真，如前面所述

知识工程

知识工程是弄清如何在人工智能中表示命题和逻辑的过程。

来看看例子：游戏Clue。

  • 在这个游戏中，一个人用一个工具在一个地方犯下了一起谋杀案
  • 人、工具、地点都用卡片表示
  • 每个类别的卡片被随机抽取并装入一个信封，由参与者来揭开谁是凶手
  • 参与者通过揭开卡片并从这些线索中推断出信封里一定有什么

我们将使用模型检查算法来揭开这个谜团。在我们的模型中，我们把我们知道的、与谋杀案有关的项目标记为真，其余的都为假。

假设我们的游戏是这样的：

  • 有三个人：芥末、梅子、猩红
  • 有三个工具：刀、左轮手枪、扳手
  • 有三个地点：舞厅、厨房、图书馆

我们可以通过添加游戏规则开始创建我们的知识库：

  1. 我们肯定的是：有一个人是凶手，使用的是一种工具，而且谋杀发生在一个地点。命题逻辑：

    • (芥末∨梅子∨猩红)
    • (刀∨左轮手枪∨扳手)
    • (舞厅∨厨房∨图书馆)

  2. 游戏开始时，每个玩家会看到一个人、一个工具、一个地点，并且得知这些与谋杀没有联系。玩家们不会共享从卡片中看到的信息。假设我们的玩家得到了芥末、厨房和左轮手枪的卡片。因此我们可以添加这些命题逻辑进我们的知识库：

    • ¬(芥末)
    • ¬(厨房)
    • ¬(左轮手枪)

  3. 在游戏的其他情况下，人们可以进行猜测，提出人、工具、地点的一种组合。假设推测是“猩红用扳手在图书馆作案”。如果这个推测是错误的，那么可以推导出以下内容：

    • (¬猩红∨¬图书馆∨¬扳手)

  4. 现在有人给我们看到了梅子的卡片，我们可以添加这个到我们的知识库：

    • ¬(梅子)

  5. 这时我们可以得出结论，凶手是猩红，因为我们有证据表明另外两个人不是

  6. 只要在增加一个知识，比如说，不是舞厅，就可以给我们更多的信息：

    • ¬(舞厅)

  7. 现在利用之前的多个数据，我们可以推断出是猩红在图书馆内用刀杀了人。然而这个猜测是错的，因为我们没有证据表明凶器具体是什么。最终的结论是刀

整个流程在Python中就是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 添加线索至知识库
knowledge = And(
    # 添加游戏起始条件
    Or(mustard, plum, scarlet),
    Or(ballroom, kitchen, library),
    Or(knife, revolver, wrench),
    
    # 添加我们所看到的第一组卡片
    Not(mustard),
    Not(kitchen),
    Not(revolver),
    
    # 添加他人举出的猜测
    Or(Not(scarlet), Not(library), Not(wrench)),
    
    # 添加我们之后得知的线索
    Not(plum),
    Not(ballroom)
)

我们还可以看看另外一个逻辑谜题：

  • 有四个不同的人：吉尔德洛依、波莫纳、密涅瓦、霍勒斯

  • 他们被分配到四个不同的学院：格兰芬多、赫夫帕夫、拉文克劳、斯莱特林

  • 每个学院正好有一个人

首先，这个谜题的条件很难被命题逻辑来表示，因为每一个可能的分配都是一个命题。其次为了表示每个人都属于某个学院，就需要Or()来包含所有每个人可能的学院分配情况。接着，为了说明如果有一个人被分配到一个学院，他们就不会被分配到其他学院，我们还要给每个人写一大堆命题。

另一种可以用命题逻辑解决的谜题是Mastermind。

  • 玩家1按照一定的顺序排列颜色，玩家2要猜出该顺序
  • 每个回合里，玩家2做出猜测，玩家1给出一个数字，表示玩家2猜对了多少种颜色
  1. 假设玩家2猜测“红蓝绿黄”，玩家1给出数字2
  2. 玩家2仅切换2个颜色的位置：“蓝红绿黄”，玩家1给出数字0
  3. 借此得知，红蓝原先的位置是正确的，这时切换另外2个颜色的位置：“红蓝黄绿”，玩家1给出数字4，代表游戏结束。
  • 用命题逻辑来表示这一点，需要我们有 (颜色的数量)2(\text{颜色的数量})^2 个原子命题。因此在有四种颜色的情况下，我们将有红0、红1、红2、红3、蓝0……这些命题代表着颜色和位置
  • 用命题逻辑表示游戏规则，也就是每个位置只有一种颜色，而且没有颜色重复，并将其加入知识库
  • 最后将我们拥有的所有线索添加到知识库中

推理规则

模型检查不是一种有效的算法，因为它必须在给出答案之前考虑每一种可能的模型。

如果是KB为真的模型，那么查询R也是真的

推理规则允许我们在现有知识的基础上生成新的信息，而无需考虑每一个可能的模型。推理规则通常使用一个横条来表示，横条将上面的部分（前提）和下面的部分（结论）分开。前提是我们拥有的任何知识，而结论是基于前提可以产生的知识。

Modus Ponens Example

肯定前件

肯定前件（Modus Ponens）就是在我们知道一个暗示、其前项是真的，那么后项也是真的。

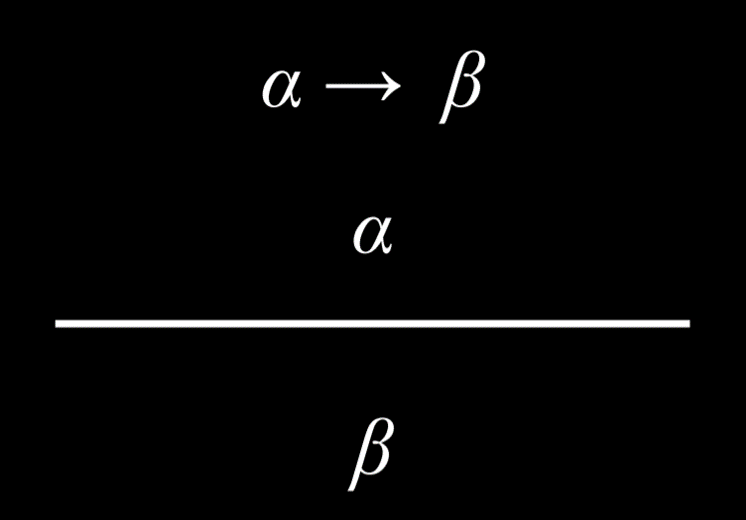
Modus Ponens

连词消除

也被称为和消除（And Elimination）。

如果一个“和”的命题为真，那么其中任何一个原子命题也是真。

例子：

  • 已知：哈利是罗恩和赫敏的朋友
  • 结论：哈利是赫敏的朋友

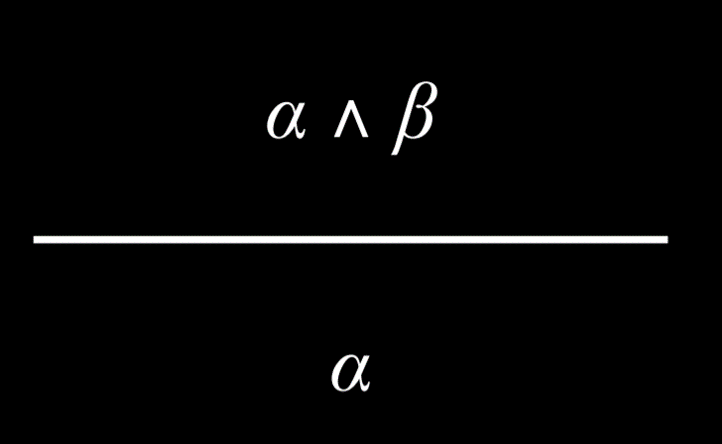
And Elimination

双重否定

一个命题如果被否定了两次，那它就是真。

例子：哈利没有通过考试是不真实的。

  1. (哈利没有通过考试)是不真实的
  2. ¬(哈利没有通过考试)
  3. ¬(¬(哈利没有通过考试))
  4. 双重否定抵消了彼此，让该命题“哈利通过了考试”变为真

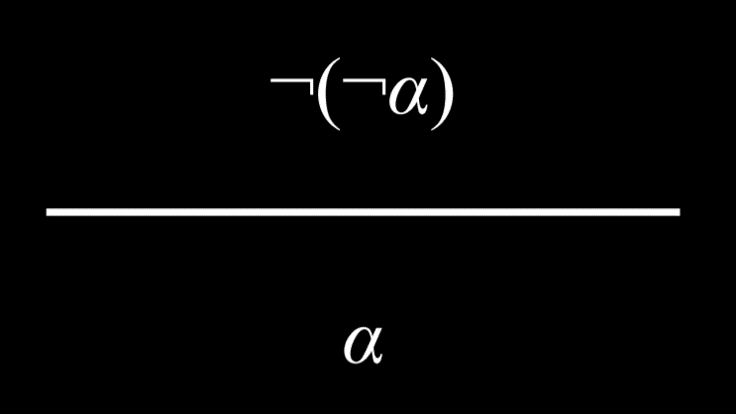
Double Negation Elimination

暗示消除

暗示相当于被否定的前项和后项之间的“或”关系。

例子：以下等同于彼此

  • 如果下雨了，那么哈利在室内
  • (没有下雨)或(哈利在室内)

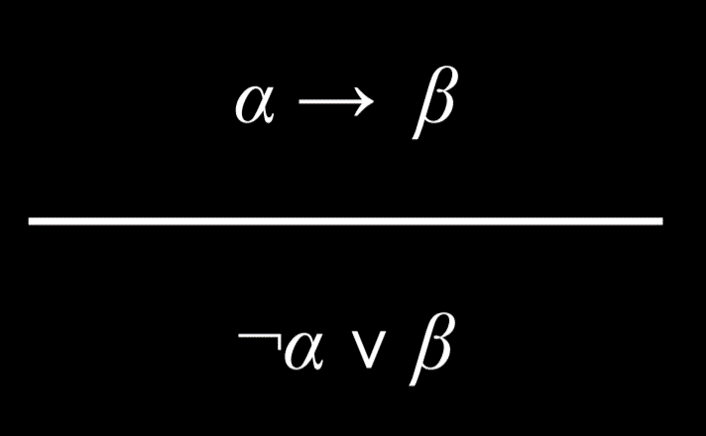
Implication Elimination

由于P→Q和P∨Q有相同的真值分配，因此在逻辑上是等价的。

另一种思考方式是如果满足两个可能的条件中的任何一个，暗示就是真的：

  1. 如果前项为假，那么暗示为真
    • ¬P∨Q：如果P为假，那么这个命题总是真的
  2. 如果前项为真，只有当后项为真时，暗示才为真
    • 如果P和Q都是真，那么¬P∨Q就为真
    • 如果P为真，Q为假，那么¬P∨Q就为假

双条件消除

一个双条件命题等同于一个暗示命题和其翻转命题用“和”连接在一起。

例子：以下等同于彼此。

  • 只有在哈利在室内的时候，外面才会下雨
  • (如果下雨了，那么哈利在室内)和(如果哈利在室内，那么外面在下雨)

Biconditional_Elimination

德摩根定律

有可能把一个“和”连接词变成一个“或”连接词。例如：“哈利和罗恩都通过了测试，这不是真的”，可以得出结论：“哈利通过考试不是真的”或者“罗恩通过考试不是真的”。也就是说，要使前面的“和”命题为真，“或”命题中的至少一个命题必须为真。

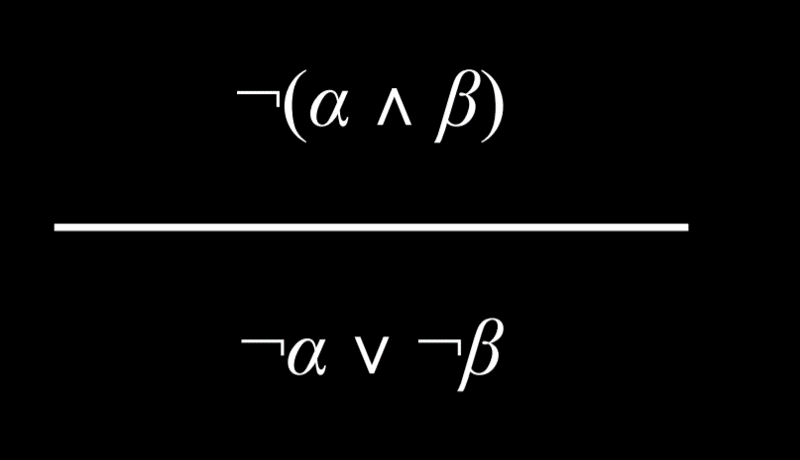
De Morgan's 1

同样地，也可以得出相反的结论。例如命题“哈利或罗恩通过测试是不真实的”可以被改写为“哈利没有通过测试”和“罗恩没有通过测试”。

分配律

一个由两个元素组成的命题，如果使用“和”或“或”连接词来分组，那就可以被分配或分解成由“和”和“或”组成的更小的单元。

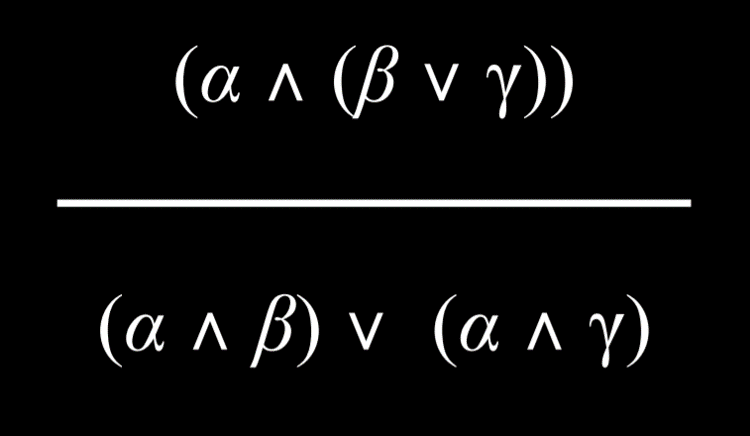
Distributive 1

知识和搜索问题

推理可以被看作是一个具有以下属性的搜索问题：

  • 初始状态：起始初始库
  • 行动：推理规则
  • 过渡模型：推理中的新知识库
  • 目标测试：检查我们要证明的语句是否在知识库内
  • 路径成本函数：证明中的步骤数量

这些都表示了搜索算法的多功能性，使我们能够在现有知识的基础上利用推理规则得出新的信息。

归结原理

归结原理（resolution）是一个强大的推理规则。如果“或”命题中的两个原子命题中的一个为假，那么另外一个就必须为真。

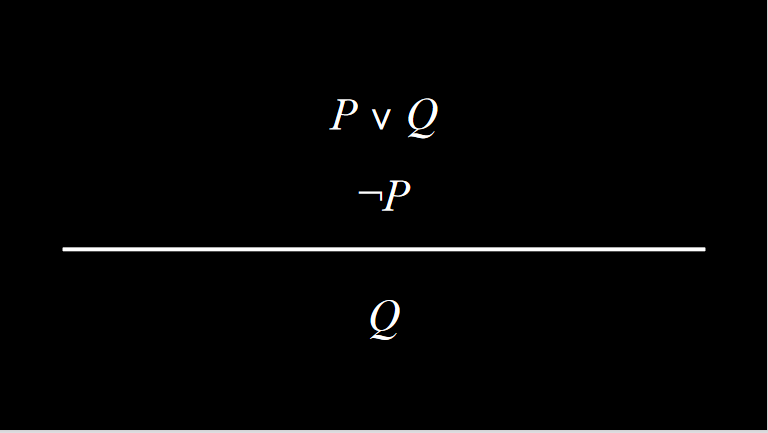
Resolution

归结原理依赖于互补文字（complementary literals），即两个相同的原子命题，其中一个被否定，另一个没有被否定。

Resolution

互补文字使我们能够通过解析推理产生新的句子。因此推理算法通过定位互补文字来生成新的知识。

一个从句是一个字词的二元链接（一个命题符号或者一个命题符号的否定）。分句由一个“或”逻辑连接词（P∨Q∨R）连接。另一方面，连词由“和”逻辑连接词相连的的命题组成（P^Q^R）。

分句允许我们把任何逻辑语句转换成合取范式（CNF），也就是分句的连接，例如：

  • (A∨B∨C)^(D∨¬E)^(F∨G)

将命题转换为合取范式的步骤：

  1. 消除双条件；将α↔β变成(α→β)^(β→α)
  2. 消除暗示；将α→β变成¬α∨β
  3. 使用德摩根定律，将否定向内移动，直到只有文字被否定；将¬(α∨β)变为¬α∨¬β

更多的例子：(P∨Q)→R

  1. ¬(P∨Q)∨R，消除暗示
  2. (¬P∨¬Q)∨R，德摩根定律
  3. (¬P∨R)^(¬Q∨R)，分配律

在这一点上，我们可以对合取范式运行推理算法。偶尔在解析推理的过程中我们会遇到这样的情况：一个子句包含两次相同的文字。我们会需要使用一个叫做分解（factoring）的过程，将重复的文字删除。

例子：

(P∨Q∨S)^(¬P∨R∨S)允许我们通过解析推断(Q∨S∨R∨S)。重复的S会被删除，得到(Q∨R∨S)。

消除一个文字和它的否定，也就是¬P和P，可以得到空的分句。空句总是假，因为P和¬P不可能都是真：

  • 确定KB是否⊨α：
    • 检查：(KB^¬α)是否是矛盾的？
      • 如果是，则KB⊨α
      • 如果否，则没有蕴含关系

矛盾证明是计算机科学中经常使用的一种工具。如果我们的知识库为真，而它与¬α相矛盾。这意味着¬α为假。因此α绝对为真。

  • 确定KB是否⊨α：
    • 将(KB^¬α)转换为合取范式
    • 继续检查，看我们能否用归结原理产生一个新的分句
    • 如果产生了一个空句，代表我们得到了一个矛盾，从而证明KB⊨α
    • 如果没有产生矛盾，也没有更多的子句可以被推断出来，也就没有蕴含关系

例子：(A∨B)^(¬B∨C)^(¬C)是否蕴含A？

  1. 用矛盾法证明。假设A为假，那就会得出(A∨B)^(¬B∨C)^(¬C)^(¬A)
  2. 既然我们知道C为假（因为¬C），那么(¬B∨C)的唯一可能是B也是假的，这样¬B就为真（将¬B加入到我们的知识库）
  3. (A∨B)的唯一可能是A为真（将A加入我们的知识库）
  4. 现在知识库中有两个互补的文字：A和¬A。我们得到了一个空的集合，根据定义，空的集合为假，所以我们得到了一个矛盾

一阶逻辑

一阶逻辑（First-Order Logic）是另一种类型的逻辑，它允许我们比命题逻辑更简洁地表达更复杂的想法。一阶逻辑使用两种类型的符号：常量符号和谓词符号。

  • 常量符号代表对象
  • 谓词符号更像是关系或函数，接受一个参数并返回一个真或假的值

回到逻辑谜题：在霍格沃茨有不同的人和房子的分配。常量符号是人或者学院，而谓词符号就是一些持有常量符号真或假的属性。

例子：

  • 使用句子Person(Minerva)来表达Minerva是一个人
  • 使用句子House(Gryffindor)来表达格兰芬多是一个学院

所有的逻辑连接词在一阶逻辑中的使用方式与命题逻辑的相同。

例子：

  • ¬House(Minerva)表达了Minerva不是一个学院

一个谓词符号也可以接受两个或以上的参数，并表达它们之间的关系。

例子：

  • BelongsTo表达了两个参数之间的关系，即人和人所属的房子
  • Minerva属于格兰芬多可以写成：BelongsTo(Minerva, Gryffindor)

全称量化

量化是一种工具，可以在一阶逻辑中用来表示句子而不使用特定的常数符号。全称量化使用符号∀来表达”对于所有“（for all）。

例子：∀x.BelongsTo(x, Gryffindor) -> ¬BelongsTo(x, Hufflepuff)，表达了对于所有符号来说，如果这个符号属于格兰芬多，那么它就不属于赫夫帕夫。

存在量化

存在量化是一个与全称量化平行的概念。然而，全称量化被用来创建对所有x都为真的句子，存在量化被用来创建对至少一个x为真的句子。存在量化使用符号∃来表示。

例子：∃x.House(x)^BelongsTo(Minerva, x)，意味着至少有一个符号既是学院，Minerva也属于它。

换句话说，这表达了Minerva属于一个学院的想法。

存在量化和全称量化可以在同一个句子中使用。

例子：∀x.Person(x) -> (∃x.House(y)^BelongsTo(x,y))表达的意思是如果x是一个人，那么至少有一个学院y是这个人的归属。

换句话说，这个句子意味着每个人都属于一个学院。

测验

  1. 考虑以下逻辑句子：

    1. 如果赫敏在图书馆内，那么哈利就在图书馆内
    2. 赫敏在图书馆内
    3. 罗恩在图书馆并且罗恩不在图书馆内
    4. 哈利在图书馆内
    5. 哈利不在图书馆内或赫敏在图书馆内
    6. 罗恩在图书馆内或赫敏在图书馆内

    哪个逻辑蕴含为真：

    • 句子6蕴含了句子3
    • 句子6蕴含了句子2
    • 句子2蕴含了句子5
    • 句子5蕴含了句子6
    • 句子1蕴含了句子4
    • 句子2蕴含了句子2

  2. 表达式A⊕B表示句子"A或B，但不是全部为真"。以下哪个在逻辑上等同于A⊕B：

    • (A ∨ B) ∧ ¬ (A ∧ B)
    • (A ∨ B) ∧ (A ∧ B)
    • (A ∧ B) ∨ ¬ (A ∨ B)
    • (A ∨ B) ∧ ¬ (A ∨ B)

    答案：(A ∨ B) ∧ ¬ (A ∧ B)

    解析：(A或者B) 和 不是(A和B)

  3. R是”现在下雨“，C是”现在多云“，S是”现在晴天“。哪个表达了”如果现在下雨，那么现在是多云而不是晴天“：

    • (R → C) ∧ ¬S

    • R → C → ¬S

    • R ∧ C ∧ ¬S

    • R → (C ∧ ¬S)

    • (C ∨ ¬S) → R

    答案：R → (C ∧ ¬S)

    解析：(现在下雨) 暗示 (现在多云 和 不是(现在晴天))

  4. Student(x)代表了”x是一个学生“；Course(x)代表了”x是一个课程“；Enrolled(x,y)代表了”x入学了y“。哪个一阶逻辑句子代表了”哈利和赫敏同时入学了的课程“：

    • ∃x. Enrolled(Harry, x) ∨ Enrolled(Hermione, x)

    • ∀x. Enrolled(Harry, x) ∨ Enrolled(Hermione, x)

    • ∀x. Course(x) ∧ Enrolled(Harry, x) ∧ Enrolled(Hermione, x)

    • ∃x. Course(x) ∧ Enrolled(Harry, x) ∧ Enrolled(Hermione, x)

    • ∀x. Enrolled(Harry, x) ∧ ∀y. Enrolled(Hermione, y)

    • ∃x. Enrolled(Harry, x) ∧ ∃y. Enrolled(Hermione, y)

    答案：∃x. Course(x) ∧ Enrolled(Harry, x) ∧ Enrolled(Hermione, x)

    解析：(x是一个课程) 和 (哈利入学了x) 和 (赫敏入学了x)；存在量化：至少有一个课程，并且哈利属于它，赫敏也属于它

作业Knights

1978年，逻辑学家Raymond Smullyan出版了《这本书叫什么名字？》。这是一本逻辑谜题书。在这本书中，有一类谜题被Smullyan称作为”骑士和无赖“（Knights and Knaves）。

在这个谜题中，以下信息被给出：

  • 每个角色要么是骑士，要么就是无赖
  • 骑士总是说真话，而无赖总是撒谎

这个迷题的目的是，给定一组由每个角色说出的句子，对于每个角色，确定该角色是骑士还是无赖。

例如单个角色A，它说”我既是骑士也是无赖“。根据逻辑，我们可以推断这句话不可能为真。因此A一定是无赖。

分发代码

瞅瞅logic.py文件，它定义了一些用于不同类型的逻辑连接词的类。这些类可以互相组成，例如And(Not(A), Or(B, C))这样的表达式代表了一个逻辑句子，说明A不是真的，而B或C是真。

该文件还有一个函数model_check()，它接收一个知识库和一个查询作为参数。知识库是一个单一的逻辑句子：如果多个逻辑句子是已知的，它们就可以被连接到一个And()中。model_check()递归地考虑了所有可能的模型。如果知识库包含了查询，就返回True，否则返回False。

现在来看看puzzle.py。在顶部有六个命题符号被定义，例如AKnight表示”A是一个骑士“，而AKnave表示”A是一个无赖“。我们也同样为人物B和C定义了命题符号。

下面还有四个不同的知识库：knowledge0、knowledge1、knowledge2、knowledge3，它们将分别包含推导谜题所需的知识。

puzzle.py的主函数在所有谜题上循环，并使用模型检查来计算，给定该谜题的知识并打印出模型检查算法能够得出的任何结论。

目标

将知识添加到知识库中，以解决下列谜题：

  1. A说”我既是骑士也是无赖“
  2. A说”我们都是骑士“；B没有说话
  3. A说“我们是同类人”；B说“我们是不同类的人”
  4. A要么说了“我是一个骑士”，要么说了“我是一个无赖”，但是你不知道；B说“A说了他是一个无赖”；C说“A是一个骑士”

作业minesweeper

扫雷是一个益智游戏，由一个单元格组成，其中一些单元格中隐藏着地雷。点击含有地雷的单元格会引爆地雷，并导致用户输掉游戏。点击一个安全的单元格会显示一个数字，表明有多少个相邻的单元格含有炸弹。

命题逻辑

你在这个项目中的目标是建立一个能玩扫雷游戏的人工智能。我们可以用一种方法来表示人工智能对扫雷游戏的了解，那就是让每个单元格成为一个命题变量，如果该单元格含有地雷，则为真，否则就是假。

人工智能会知道每次点击安全的单元格时显示的数字。

Middle cell with labeled neighbors

用上图作为例子，我们知道八个相邻的单元格中会有一个是地雷。因此我们可以写一个像下面这样的逻辑表达式来表示相邻单元格中的一个是地雷：Or(A,B,C,D,E,F,G,H)。

但实际上我们知道的要比这个表达式所说的要多。上面这个逻辑句子表达的是这八个变量中至少有一个是真的，但我们可以做一个比这更有力的声明：我们知道这八个变量中只有一个是真的。那就是：

1
2
3
4
5
6
7
8
9
10
Or(
    And(A, Not(B), Not(C), Not(D), Not(E), Not(F), Not(G), Not(H)),
    And(Not(A), B, Not(C), Not(D), Not(E), Not(F), Not(G), Not(H)),
    And(Not(A), Not(B), C, Not(D), Not(E), Not(F), Not(G), Not(H)),
    And(Not(A), Not(B), Not(C), D, Not(E), Not(F), Not(G), Not(H)),
    And(Not(A), Not(B), Not(C), Not(D), E, Not(F), Not(G), Not(H)),
    And(Not(A), Not(B), Not(C), Not(D), Not(E), F, Not(G), Not(H)),
    And(Not(A), Not(B), Not(C), Not(D), Not(E), Not(F), G, Not(H)),
    And(Not(A), Not(B), Not(C), Not(D), Not(E), Not(F), Not(G), H)
)

嗯……是不是太复杂了？这只是为了表达一个单元格中有1。如果单元格中有2或者3或者其他的值，表达式可能会更长。

试图对这种类型的问题进行模型检查，也会很快变得难以解决：在一个8x8的网格上，也就是简单模式会用的尺寸，我们会有64个变量，因此有 2642^{64} 个可能的模型需要检查。对于一台计算机来说，在任何合理的时间内计算的数量都太多了。对于这个问题，我们需要一个更好的知识来表示。

知识表示

又称知识重呈、知识表现、知识表征……

我们将像这样表示人工智能的每一句知识：{A,B,C,D,E,F,G,H}=1。

这个表达式中的每个逻辑句子都有两个部分：黑板上涉及该句子的一组单元格，以及一个数字计数，代表这个单元格中有多少是地雷的计数。上面的逻辑句子表示了“在这八个单元格中正好有一个是地雷”。

分发代码

这个项目有两个主要文件：runner.py和minesweeper.py。前者已被实现，后者包含了游戏本身和AI玩游戏的所有逻辑。

minesweeper.py定义了三个类：Minesweeper、Sentence、MinesweeperAI。第一个处理游戏的玩法，第二个表示一个逻辑句子，第三个处理根据知识推断出要做的动作。

Minesweeper类已被实现。每个单元格是一对(i,j)，其中i是行号（从0到高度-1），j是列号（从0到宽度-1）。

Sentence类被用来表示背景中描述的逻辑句子的形式。每个句子中都有一组单元格，以及这些单元格中有多少个地雷的计数。该类还包含函数known_mines()和known_safes()用于确定句子中的任何单元格是否为已知的地雷或已知的安全区。它还包含了mark_mine()和mark_safe()用来更新句子，以应对关于一个单元格的新信息。

最后，MinesweeperAI类将实现一个可以玩扫雷的AI。这个AI类记录了一些数值：

  • self.moves_made包含了一个装有所有已经点击过的单元格的集合，所以AI知道不要再去选择那些单元格
  • self.mines包含了一个装有所有已知是地雷的单元格的集合
  • self.safes包含了一个装有所有已知是安全的的单元格的集合
  • self.knowledge包含了一个装有所有人工智能已知为真的句子的列表

mark_mine()将一个单元格添加到self.mines中。mark_safe()同理。

2. Uncertainty

在现实里，人工智能往往只拥有对世界的部分知识，剩余的空间则都是不确定性（uncertainty）。尽管如此，我们仍希望我们的人工智能在这些情况下做出最佳的决策。

  • 例如：在预测天气时，人工智能能拥有今天的天气信息，但无法百分之百准确地预测明天的天气

不过我们还是可以在有限信息和不确定性地情况下创建出可以做出最佳决策的人工智能。

概率

不确定性可以被表示为一些事件及其发生的可能性或概率。

可能的世界

每种可能的情况都可以被看作是一个世界，用小写希腊字母 ω 来表示。

  • 例如：投掷骰子时可以产生六个可能的世界

为了表示某个世界的概率，我们使用 P(ω)。

概率的公理

概率的公式为 0 < P(ω) < 1，每个表示概率的值必须在 0 和 1 之间。0 是不可能发生的事件，比如投掷骰子时得到了点数 7；1 是一定会发生的事件，比如投掷一个标准骰子得到一个小于 10 的点数。通常值越高，事件发生的可能性就越大。每个可能事件的概率加起来等于 1。

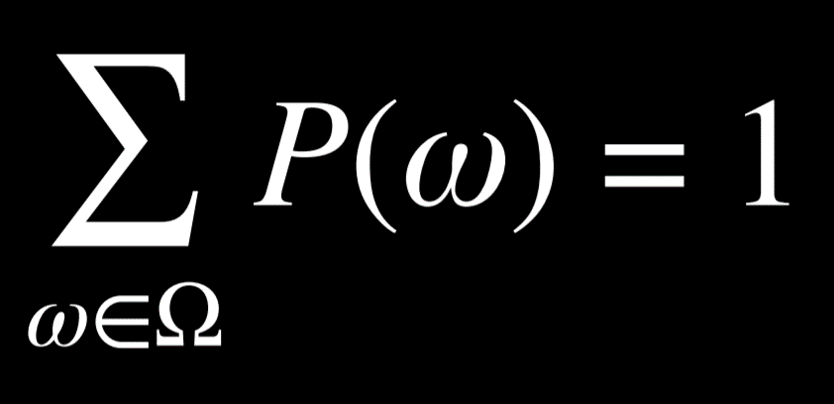
Summing Probabilities

用标准骰子掷出一个数字 R 的概率可以表示为 P(R)。在我们的例子中，P(R) = 1/6，因为有六个可能的世界，每个都同样可能发生。现在考虑一下投掷两个骰子的事件，一下就有了 36 种可能的事件。

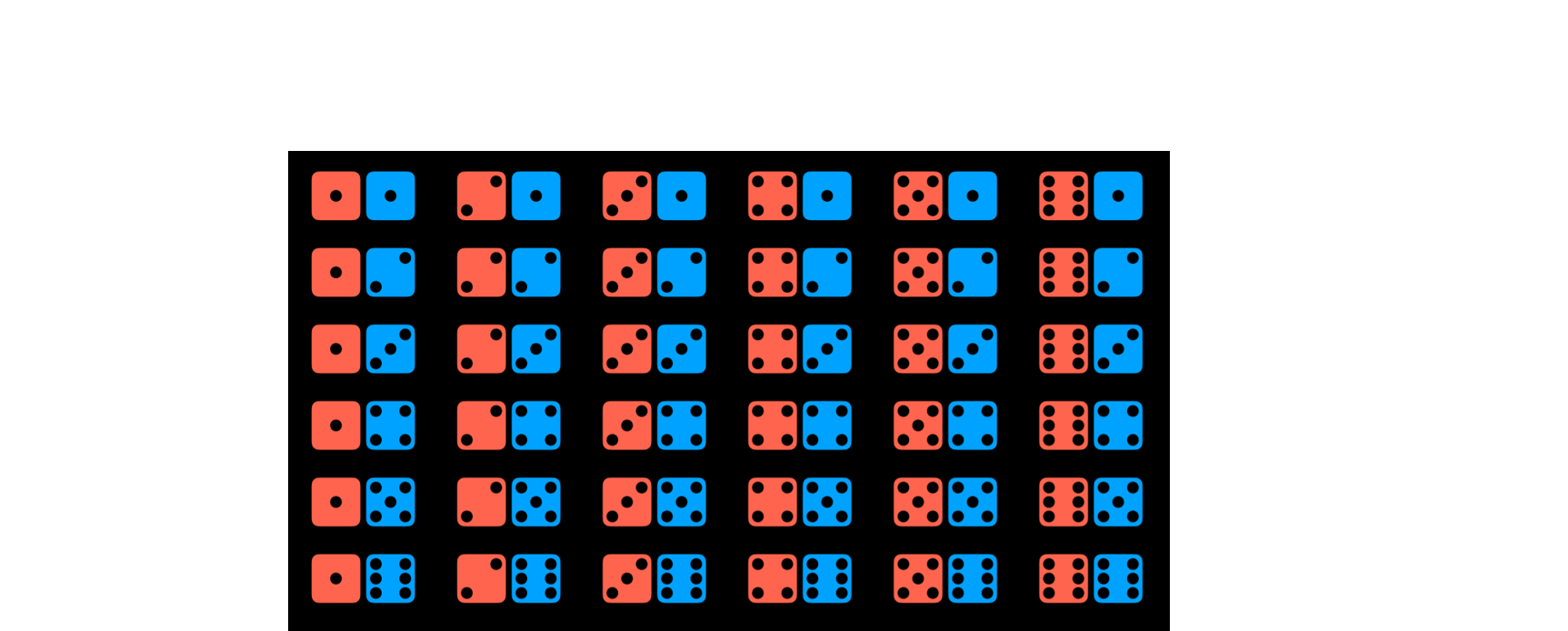
36 Events

但是，如果我们试图预测两个骰子的和会发生什么？在这种情况下，我们只有 11 个可能的值。

Sum of Two Dice

要得到一个事件的概率，我们要将它发生的世界数除以所有可能的世界数。例如，投掷两个骰子时会有 36 个可能的世界。只有在其中一个世界里，当两个骰子都掷出 6 时，我们才能得到 12 的总和。因此 P(12) = 1/36。

  • 例子：P(7) 的概率是多少？7 出现在六个世界中，因此 P(7) = 6/36 = 1/6

无条件概率

无条件概率是在没有其他证据的情况下对一个命题的信度。我们迄今为止提出的所有问题都是无条件概率的问题，因为掷骰子的结果不依赖于先前的事件。

条件概率

条件概率是在已经揭示了一些证据的情况下对一个命题的信度。如前言所述，人工智能可以利用部分信息对未来做出有根据的猜测。为了使用这些信息，它们会影响事件在未来发生的概率，我们依赖于条件概率。

条件概率用 P(a | b) 来表示，意思是“在我们知道事件 b 已经发生的情况下，事件 a 发生的概率”。

  • 例如：如果昨天下雨了，今天下雨的概率是多少？ -> P(今天下雨 | 昨天下雨)

Conditional Probability Formula

换句话说，给定 b 为真的 a 的概率等同于 a 和 b 都为真的概率除以 b 的概率。

一种直观的推理方法是这样的：“我们对 a 和 b 都为真的事件感兴趣（分子），但只来自我们知道 b 为真的世界（分母）”

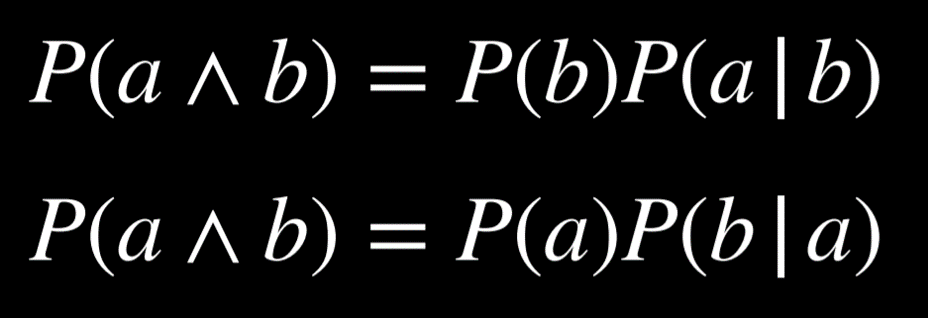
Equivalent Formulas

计算一下 P(总和为12 | 在骰子上掷出6)。首先我们要把我们的世界限制在第一个骰子的点数为 6 的世界。其次我们要得出在我们限制了问题的世界中，事件 a（总和为 12）发生了多少次（除以 P(b)，即第一个骰子掷出 6 的概率）。

Conditioned Probability

随机变量

随机变量是概率论中具有可能取值域的变量。

  • 例如：为了表示掷骰子时的可能结果，我们可以定义一个随机变量 Roll，它可以取值 {0, 1, 2, 3, 4, 5, 6}；为了表示航班的状态，我们可以定义一个变量 Flight，它可以取值 {准时, 延误, 取消}
  • 通常我们会对每个值发生的概率感兴趣，这一点可以使用概率分布来表示：
    • P(Flight = 准时) = 0.6
    • P(Flight = 延误) = 0.3
    • P(Flight = 取消) = 0.1
  • 概率分布可以更简洁地表示为向量：
    • P(Flight) = <0.6, 0.3, 0.1>
  • 为了使这种表示法可解释，值必须有一个固定的顺序（在我们的例子里，就是准时、延误、取消）

独立性

独立性指的是一个事件的发生不影响另一个事件的概率。

  • 例如：当投掷两个骰子时，每个骰子的结果都与另一个骰子独立。这与依赖事件相反，比如早上的云和下午的雨（如果早上多云，那么下午下雨的可能性就更大）

独立性可以用数学定义：当且仅当 a 和 b 的概率等于 a 的概率乘以 b 的概率时，事件 a 和 b 是独立的：P(a ∧ b) = P(a)P(b)。

贝叶斯定理

贝叶斯定理通常用于概率论中计算条件概率。给定 a 的 b 的概率等于给定 b 的 a 的概率乘以 b 的概率，除以 a 的概率。

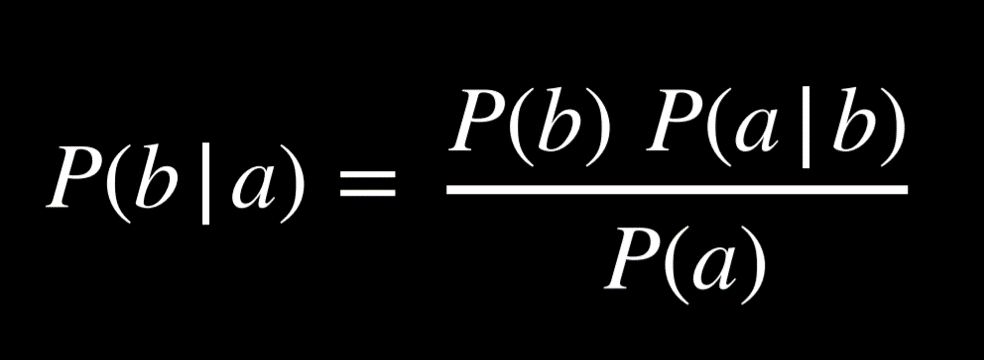
Bayes' Rule

  • 例如：计算如果早上有云，下午下雨的概率（也就是 P(雨 | 云)）
    • 80% 的下午下雨始于早晨的多云，即 P(云 | 雨)
    • 40% 的日子是早上多云，即 P(云)
    • 10% 的日子是下午下雨，即 P(雨)
  • 应用贝叶斯定理，(0.1)(0.8)/(0.4) = 0.2。也就是说，如果早上多云，那么下午下雨的概率为 20%

知道了 P(a | b) 后还可以让我们计算出 P(b | a)。知道一个可见效果给定一个未知原因的条件概率（P(可见效果 | 未知原因)）可以让我们计算出未知原因给定可见效果的概率（P(未知原因 | 可见效果)）。

  • 例如：我们可以通过医学试验来了解 P(医学检查结果 | 疾病)，在那里我们测试患有疾病的人并看看测试多久能检测到。知道这一点，我们可以计算出 P(疾病 | 医学检查结果)，即宝贵的诊断信息

联合概率

联合概率是多个事件都发生的可能性。考虑一下关于早上多云和下午下雨的概率的例子：

  • C = cloud，0.4
  • C = ¬cloud，0.6
  • R = rain，0.1
  • R = ¬rain，0.9

我们无法说早上多云是否与下午下雨的可能性有关。为了能够这样做，我们需要看两个变量的所有可能结果的联合概率：

C = cloud C = ¬cloud
R = rain 0.08 0.02
R = ¬rain 0.32 0.58

使用联合概率，我们可以推导出条件概率。

  • 例如：我们对下午下雨时早上多云的概率分布感兴趣。P(C | 雨) = P(C, 雨)/P(雨)（在概率中，逗号和 ∧ 可以互换使用）
    • 在最后一个方程中，可以将 P(雨) 视为乘以 P(C, 雨) 的某个常数
    • 因此我们可以重写 P(C, 雨)/P(雨) = αP(C, 雨) 或 α<0.08, 0.02>
    • 提取 α 后，我们得到了 C 在下午下雨时可能值的概率比例
    • 也就是说，如果下午下雨，那么早上多云和早上没有云的概率比例是 0.08 : 0.02
      • 注意 0.08 和 0.02 并不加起来等于 1；然而，由于这是随机变量 C 的概率分布，我们知道它们应该加起来等于 1
      • 因此，我们需要通过计算 α 使 α0.08 + α0.02 = 1 来归一化这些值。最后，我们可以说 P(C | 雨) = <0.8, 0.2>

概率规则

  • 否定：P(¬a) = 1 - P(a)

    • 源于所有可能的世界的概率总和为 1，而补充文字 a 和 ¬a 包括了所有的可能的世界

  • 容斥：P(a ∨ b) = P(a) + P(b) - P(a ∧ b)

    • a 或 b 为真的世界等于所有 a 为真的世界加上 b 为真的世界
    • 然而在这种情况下，有些世界会被多次计算（即 a 和 b 都为真的世界）。为了消除这种重叠，我们减去一次 a 和 b 都为真的世界
      • 例如：我有 80% 的时间吃冰淇淋、70% 的时间吃饼干。如果我们在计算今天吃冰淇淋或饼干 P(冰淇淋 ∨ 饼干)时不减去 P(冰淇淋 ∧ 饼干)，我们就会错误地得到 0.7 + 0.8 = 1.5，这与概率在 0 和 1 之间的公理相互矛盾

  • 边缘化：P(*a*) = P(*a, b*) + P(*a, ¬b*)

    • b 和 ¬b 是不相交的概率，或者说，b 和 ¬b 同时发生的概率是 0。我们也知道 b 和 ¬b 加起来是 1。因此当 a 发生时，b 可以发生也可以不发生。当我们取 a 和 b 时发生的概率加上 a 和 ¬b 同时发生的概率时，我们最终得到了 a 的概率

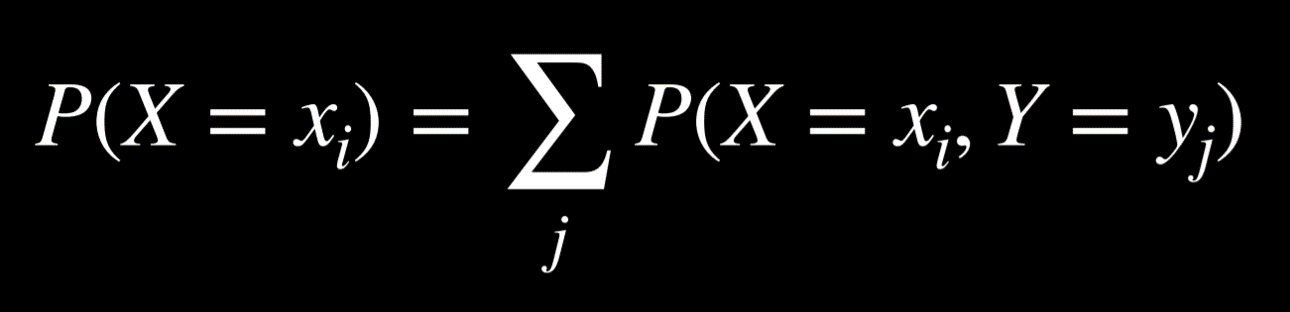
    • Marginalization

      这个方程的左边意味着”随机变量 X 取值为 xᵢ 的概率“

      • 例如：对于我们前面提到的变量 C，两个可能的值分别是早上多云和早上没云

      方程的右边则是”xᵢ 和随机变量 Y 的每个值的所有联合概率之和“

      • 例如：P(C = 多云) = P(C = 多云, R = 下雨) + P(C = 多云, R = ¬下雨) = 0.08 + 0.32 = 0.4

  • 条件化：P(a) = P(a | b)P(b) + P(a | ¬b)P(¬b)

    • 与边缘化相似，事件 a 发生的概率等于给定 b 的 a 的概率乘以 b 的概率，加上给定 ¬b 的 a 的概率乘以 ¬b 的概率

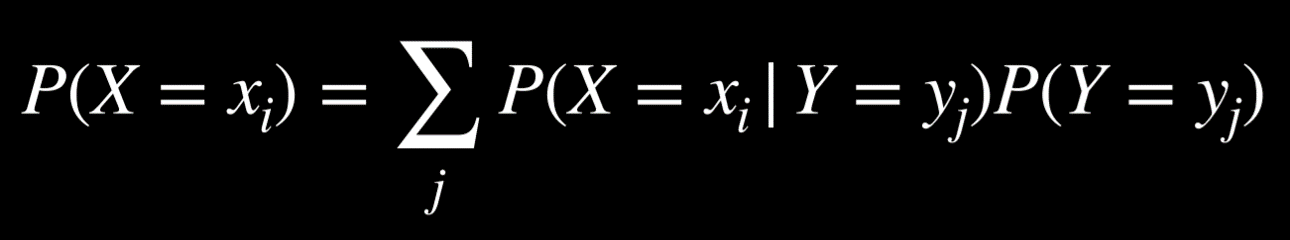
    • Conditioning

      随机变量 X 以概率等于 xᵢ 给定随机变量 Y 的每个值的概率之和乘以变量 Y 取该值的概率。记住 P(a | b) = P(a, b)/P(b)，如果我们将这个表达式乘以 P(b)，我们就会得到 P(a, b)，之后的步骤便和边缘化一样

贝叶斯网络

贝叶斯网络是一种表示随机变量之间依赖关系的数据结构，其特性如下：

  • 是有向图，图上的每个节点都代表一个随机变量
  • 从 X 到 Y 的箭头表示 X 是 Y 的父节点，即 Y 的概率分布取决于 X 的值
  • 每个节点 X 都有概率分布 P(X | Parents(X))

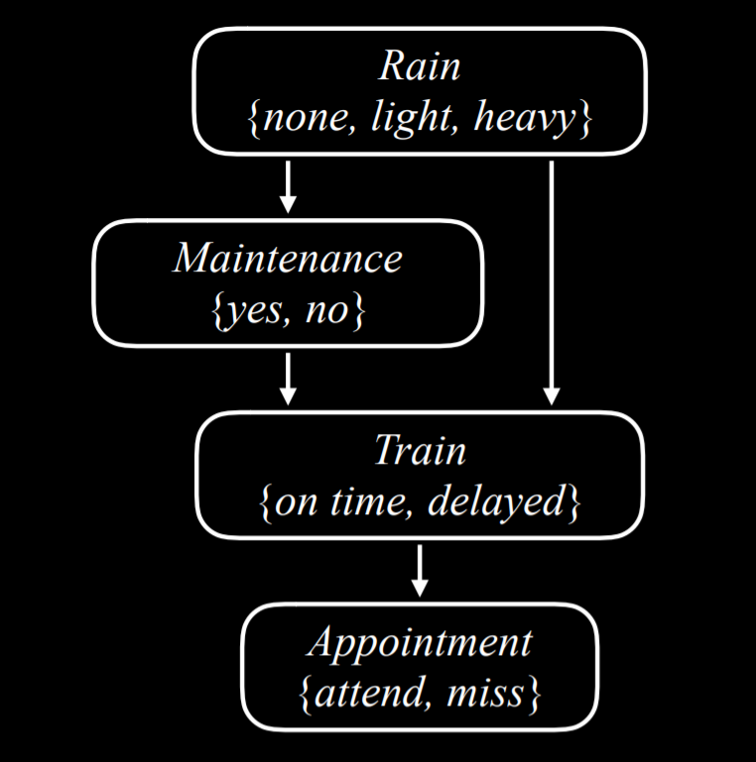
考虑这个例子，它涉及影响了我们是否按时赴约的变量：

Bayesian Network

  • Rain 是这个网络中的根节点。这意味着它的概率分布不依赖于任何先前的事件。在我们的例子中，Rain 是一个随机变量，可以取值 {none, light, heavy}，具有以下概率分布：

    值 概率
    none 0.7
    light 0.2
    heavy 0.1

  • 在我们的例子中，Maintenance 编码是否有火车轨道维护，取值 {yes, no}。Rain 是Maintenance 的父节点，这意味着 Maintenance 的概率分布受 Rain 的影响

    none light heavy
    yes 0.4 0.2 0.1
    no 0.6 0.8 0.9

  • Train 变量编码火车是否准时或延误，取值 {on time, delayed}。注意，Maintenance 和 Rain 都有箭头指向 Train，这意味着它们都是 Train 的父节点，它们的值会影响 Train 的概率分布

    none + yes none + no light + yes light + no heavy + yes heavy + no
    on time 0.8 0.9 0.6 0.7 0.4 0.5
    delayed 0.2 0.1 0.4 0.3 0.6 0.5

  • Appointment是一个随机变量，代表我们是否出席了预约，取值 {attend, miss}。它的唯一父节点是 Train

    • 根据贝叶斯网络，父节点只包括直接关系。Maintenance 确实会影响 Train 是否准时，而 Train 是否准时会影响到我们是否出席了预约。然而，最终直接影响我们出席预约的机会的是火车是否准时到达

      • 例如：如果火车准时到达，那么即使下大雨并且轨道在维修，也不会影响我们是否赶上预约
      on time delayed
      attend 0.9 0.6
      miss 0.1 0.4
      • 例如：如果我们想要找到在没有维修、没有下雨的一天，火车晚点时错过预约的概率，也就是 P(light, no, delayed, miss)，我们将计算以下内容：
        • P(light)P(no | light)P(delayed | light, no)P(miss | delayed)
        • 每个单独概率的值都可以在上面的概率分布中找到，然后将这些值相乘就能得到 P(no, light, delayed, miss)

推理

早些时候我们通过蕴涵来推理，意味着我们可以根据我们已有的信息明确地得出新信息，也可以根据概率推断新信息。虽然这无法让我们确定新信息，但可以让我们找出某些值地概率分布。

推理具有多个属性：

  • 查询变量X：我们想要计算概率分布的变量

  • 证据变量E：一个或多个一观察到的事件 e 的变量

    • 例如：我们可能观察到有轻微的雨。这个观察帮助我们计算火车延迟的概率

  • 隐藏变量Y：不是查询变量，也没有被观察过的变量

    • 例如：在火车站台上，我们可以观察到是否在下雨，但是无法得知路的下方是否有维修工作。因此在这种情况下，维修工作是一个隐藏变量

  • 目标：计算 P(X | e)

    • 例如：给予我们知道有轻微的雨的证据变量E，计算火车变量（查询变量）的概率分布

举个例子，我们想要计算在有轻微的雨和没有轨道维修的证据下、预约变量的概率分布。也就是说，我们知道有轻微的雨并且没有轨道维修，我们想要确定我们参加预约和错过预约的概率分别是多少，也就是 P(预约 | 有雨，无维修)。根据联合概率部分，我们知道我们可以将预约随机变量的可能值表示为一个比例，将 P(预约 | 有雨，无维修) 重写为 αP(预约，有雨，无维修)。如果预约的父节点只有火车变量，而没有雨或者维修，我们该如何计算预约的概率分布？

在这里，我们将使用边缘化。P(预约，有雨，无维修) 的值等同于 α[P(预约，有雨，无维修，延误) + P(预约，有雨，无维修，准时)]。

枚举推理

枚举推理是一种根据观察到的证据 e 和一些隐藏变量 Y 来找到变量 X 的概率分布的过程。

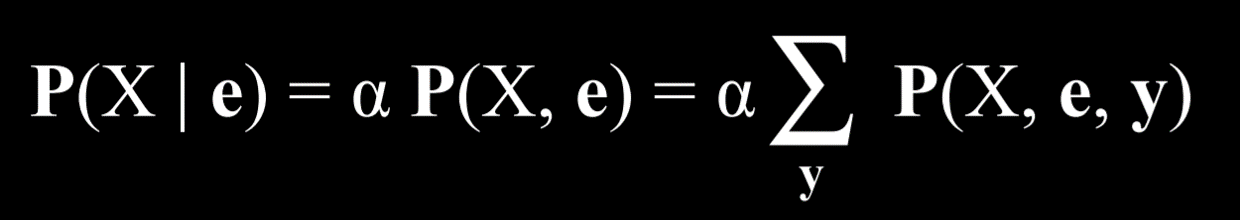
Inference by Enumeration

在这个方程中，X 代表查询变量，e 代表观察到的证据，y 代表所有隐藏变量的值，α 对结果进行归一化，使得我们得到的概率总和为1。

用文字解释这个方程，它表示给定 e 的情况下 X 的概率分布等于 X 和 e 的归一化概率分布。为了得到这个分布，我们对 X、e 和 y 的归一化概率求和，其中 y 每次取隐藏变量 Y 的不同值。

Python 中存在多个库以简化概率推理的过程。我们将使用 pomegranate 库来看看如何将上述数据表示为代码：

  1. 创建节点并为每个节点提供概率分布

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    from pomegranate import *

    # 雨节点没有父节点
    rain = Node(DiscreteDistribution({
        "none": 0.7,
        "light": 0.2,
        "heavy": 0.1
    }), name="rain")

    # 轨道维修节点是基于雨的条件概率
    maintenance = Node(ConditionalProbabilityTable([
        ["none", "yes", 0.4],
        ["none", "no", 0.6],
        ["light", "yes", 0.2],
        ["light", "no", 0.8],
        ["heavy", "yes", 0.1],
        ["heavy", "no", 0.9]
    ], [rain.distribution]), name="maintenance")

    # 火车节点是基于雨和维修的条件概率
    train = Node(ConditionalProbabilityTable([
        ["none", "yes", "on time", 0.8],
        ["none", "yes", "delayed", 0.2],
        ["none", "no", "on time", 0.9],
        ["none", "no", "delayed", 0.1],
        ["light", "yes", "on time", 0.6],
        ["light", "yes", "delayed", 0.4],
        ["light", "no", "on time", 0.7],
        ["light", "no", "delayed", 0.3],
        ["heavy", "yes", "on time", 0.4],
        ["heavy", "yes", "delayed", 0.6],
        ["heavy", "no", "on time", 0.5],
        ["heavy", "no", "delayed", 0.5],
    ], [rain.distribution, maintenance.distribution]), name="train")

    # 预约节点是基于火车的条件概率
    appointment = Node(ConditionalProbabilityTable([
        ["on time", "attend", 0.9],
        ["on time", "miss", 0.1],
        ["delayed", "attend", 0.6],
        ["delayed", "miss", 0.4]
    ], [train.distribution]), name="appointment")

  2. 通过添加所有节点来创建模型，然后通过在它们之间添加边来描述哪个节点是哪个其他节点的父节点（贝叶斯网络）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    # 创建一个贝叶斯网络并添加状态
    model = BayesianNetwork()
    model.add_states(rain, maintenance, train, appointment)

    # 给节点之间添加用来连接的边
    model.add_edge(rain, maintenance)
    model.add_edge(rain, train)
    model.add_edge(maintenance, train)
    model.add_edge(train, appointment)

    # 最终确定模型
    model.bake()

  3. 为了询问某个事件的概率有多大，我们使用我们感兴趣的值来运行模型。在这个例子中，我们想要问的是没有雨、没有轨道维修、火车准时到达并且我们准点参加会议的概率是多少

    1
    2
    3
    4
    # 基于提供的观察，计算概率
    probability = model.probability([["none", "no", "on time", "attend"]])

    print(probability)

  4. 否则我们可以使用该程序在给定一些观察到的证据时提供所有变量的概率分布。在下面的情况中，我们知道火车延误了。根据这个信息，我们计算并打印变量 Rain、Maintenance 和 Appointment 的概率分布

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    # 基于火车延误的证据进行预测计算
    predictions = model.predict_proba({
        "train": "delayed"
    })

    # 打印每个节点的预测结果
    for node, prediction in zip(model.states, predictions):
        if isinstance(prediction, str):
            print(f"{node.name}: {prediction}")
        else:
            print(f"{node.name}")
            for value, probability in prediction.parameters[0].items():
                print(f"    {value}: {probability:.4f}")

上述代码使用了枚举推理。然而这种计算概率的方式是低效的，特别是当模型中有许多变量时。另一种方法是放弃精确推理，转而采用近似推理。通过这样做，我们在生成的概率中失去了一些精度，但通常这种不精确性是可以忽略的。相反我们获得了一种可扩展的计算概率的方法。