物理学笔记，仅作为个人学习记录，不保证正确性。

1. 一维运动

位移（Displacement）是一个物体从起始点到终点的直线距离和方向。

Δx=xf−xi\Delta x = x_f - x_i

  • xfx_f：终点位置
  • xix_i：起始位置

速度（Velocity）是物体位置随时间的变化率。

vavg=ΔxΔtv_{\text{avg}} = \frac{\Delta x}{\Delta t}

  • 瞬时速度（Instantaneous velocity）是物体在某一时刻的速度

加速度（Acceleration）是速度随时间的变化率。

aavg=ΔvΔta_{\text{avg}} = \frac{\Delta v}{\Delta t}

  • 瞬时加速度（Instantaneous acceleration）是物体在某一时刻的加速度
  • 恒定加速度的情况下，v=v0+atv=v_0+at

1.1. 匀速/匀加速直线运动

假设速度随着时间呈线性变化、恒定加速度也是如此的情况（见下图）下，起始速度和终点速度的算术平均值可以用来表示任意时间间隔内的平均速度：vˉ=v0+v2\bar{v}=\frac{v_0+v}{2}。

1.png

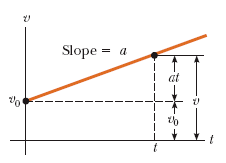
基于这个公式，我们可以推导出物体位移随时间变化的公式：

Δx=vˉt=(v0+v2)t\Delta x = \bar{v} t = (\frac{v_0+v}{2}) t

Δx=12(v0+v)t\Delta x = \frac{1}{2} (v_0+v) t

再把速度公式代入，得到：

Δx=12(v0+v0+at)t\Delta x = \frac{1}{2} (v_0 + v_0 + at) t

Δx=v0t+12at2\Delta x = v_0 t + \frac{1}{2} a t^2

如果不想要包含时间的话，可以推出：

Δx=12(v+v0)(v−v0a)=v2−v022a\Delta x = \frac{1}{2} (v + v_0) (\frac{v-v_0}{a}) = \frac{v^2-v^2_0}{2a}

v2=v02+2aΔxv^2 = v^2_0 + 2a \Delta x

1.1.1. 总结

公式 介绍
v=v0+atv=v_0+at 速度随时间的变化
Δx=v0t+12at2\Delta x = v_0 t + \frac{1}{2} a t^2 位移随时间的变化
v2=v02+2aΔxv^2 = v^2_0 + 2a \Delta x 速度和位移的关系

1.2. 自由落体

亚里士多德认为物体的速度与质量成正比，也就是说物体越重，下落的速度越快。但据说伽利略通过实验发现，不同质量的物体在没有空气阻力的情况下，下落的速度是相同的。宇航员在月球上的实验也证实了这一点。在空气阻力可以忽略不计的情况下，这种运动称为自由落体。

自由落体的加速度是一个常量，通常用gg表示，称为重力加速度。在地球表面，g=9.8 m/s2g=9.8\ m/s^2。

  • 重力加速度的方向是向下的。不过在运动方程中重力加速度为正还是负取决于我们选择的坐标系。如果我们选择向上定义为负值，那么重力加速度就是负的

自由落体的速度随时间的变化是线性的：

v=v0+gtv = v_0 + gt

自由落体的位移随时间的平方增加：

h=h0+v0t+12gt2h = h_0 + v_0 t + \frac{1}{2} g t^2

2. 二维运动

在二维空间中，位移、速度和加速度的概念与一维运动类似。不过在二维运动中，我们需要考虑两个方向上的运动，通常指的是水平方向和竖直方向。

二维位移是一个物体从起始点到终点的直线距离和方向，同时也要考虑两个方向上的变化。

Δr⃗=r⃗f−r⃗i\Delta \vec{r} = \vec{r}_f - \vec{r}_i

  • r⃗\vec{r}：位置矢量

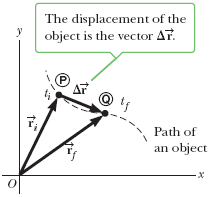
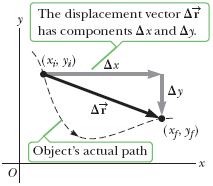
img.png

Δr⃗\Delta \vec{r}包含了Δx\Delta x和Δy\Delta y两个分量，代表着物体在Δt\Delta t时间内从(xi,yi)(x_i, y_i)到(xf,yf)(x_f, y_f)的位移。

img.png

平均速度的定义与一维运动类似：

v⃗avg=Δr⃗Δt\vec{v}_{\text{avg}} = \frac{\Delta \vec{r}}{\Delta t}

因为位移是一个矢量、时间是一个标量，所以我们可以总结出平均速度也是一个矢量、沿着Δr⃗\Delta \vec{r}的方向。

瞬时速度是其平均速度在Δt\Delta t为0时的极限：

v⃗=lim⁡Δt→0Δr⃗Δt\vec{v} = \lim_{\Delta t \to 0} \frac{\Delta \vec{r}}{\Delta t}

平均加速度：

a⃗avg=Δv⃗Δt\vec{a}_{\text{avg}} = \frac{\Delta \vec{v}}{\Delta t}

瞬时加速度：

a⃗=lim⁡Δt→0Δv⃗Δt\vec{a} = \lim_{\Delta t \to 0} \frac{\Delta \vec{v}}{\Delta t}

2.1. 二维运动

在二维运动中，物体可以同时在水平方向和竖直方向上运动。这种二维运动的一个重要特例是抛体运动（Projectile motion）。

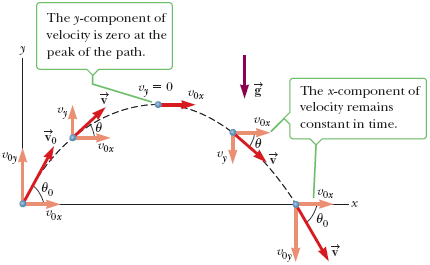
img.png

如图，物体离开地面时的抛物线轨迹速度为v⃗0\vec{v}_0，v⃗\vec{v}会随着时间增长。但是vxv_x，也就是水平方向的速度是恒定的，依旧等同于v0xv_0x。当物体到达最高点时，vyv_y呈现为0，但加速度依然等同于自由落体的加速度、方向向下。

假设物体在离开地面的时候t=0t=0、起始速度为v⃗0\vec{v}_0，且速度矢量形成了一个角度θ\theta，那么我们可以得到：

v0x=v0cos⁡θv_{0x} = v_0 \cos \theta

v0y=v0sin⁡θv_{0y} = v_0 \sin \theta

如果只考虑水平方向、水平方向的加速度恒定，那么我们可以得到：

vx=v0x+axtv_x = v_{0x} + a_x t

Δx=v0xt+12axt2\Delta x = v_{0x} t + \frac{1}{2} a_x t^2

vx2=v0x2+2axΔxv_x^2 = v_{0x}^2 + 2 a_x \Delta x

  • 以上的v0xv_{0x}等于v0cos⁡θ0v_0 \cos \theta_0

反过来只考虑垂直方向和垂直方向的加速度的话，那便是：

vy=v0y+aytv_y = v_{0y} + a_y t

Δy=v0yt+12ayt2\Delta y = v_{0y} t + \frac{1}{2} a_y t^2

vy2=v0y2+2ayΔyv_y^2 = v_{0y}^2 + 2 a_y \Delta y

  • 同理，v0yv_{0y}等于v0sin⁡θ0v_0 \sin \theta_0，且aya_y恒定

这种情况下速度vv可以使用勾股定理表示：

v=vx2+vy2v = \sqrt{v_x^2 + v_y^2}

角度θ\theta可以使用反正切函数表示：

θ=tan⁡−1vyvx\theta = \tan^{-1} \frac{v_y}{v_x}

  • 如果矢量落在第二或第三象限，那么θ\theta的值需要加上180°180°

2.2. 相对速度

相对速度将两个不同观测者的测量结果联系起来。物体的测量速度取决于观察者相对于物体的速度。例如高速公路上同方向行驶的汽车，它们相对于地球而言是高速行驶的，但相对于彼此，它们几乎没有移动。

因此，速度的测量取决于观察者的参照系。参照系只是坐标系。大多数时候，我们使用相对于地球的静止参照系，但偶尔我们也会使用与相对于地球以恒定速度运动的公共汽车、汽车或飞机相关的运动参照系。

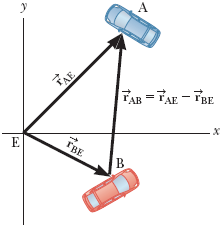
在二维空间中，相对速度的计算可能令人困惑，因此采用系统的方法非常重要和有用。假设 E 是一个观察者，相对于地球静止不动。将两辆汽车分别标记为 A 和 B，并引入以下符号：

  • rAE⃗\vec{r_{AE}}：汽车 A 相对于 E 的位移
  • rBE⃗\vec{r_{BE}}：汽车 B 相对于 E 的位移
  • vAB⃗\vec{v_{AB}}：汽车 A 相对于 B 的速度

img.png

3. 牛顿运动定律

牛顿运动定律是描述物体运动的基本规律，由牛顿在17世纪提出。这些定律是经典力学的基础，对于理解和预测物体如何在力的作用下移动至关重要。

牛顿第一定律也被称为惯性定律，它表明如果没有外力作用，物体将保持其状态不变。也就是说静止的物体将保持静止，而移动的物体将以恒定速度直线运动。

比方说，当你在车上的时候，车突然启动，你会向后倾斜。这是因为你的身体保持了静止状态，而车突然加速了。当车突然停下来的时候，你会向前倾斜。这是因为你的身体保持了前进的状态，而车突然停下了。

牛顿第二定律是最重要的定律之一，它表明力（Force）等于物体的质量乘以加速度，或者说物体的加速度是力和质量的商。

F⃗=ma⃗\vec{F} = m \vec{a}

这个定律解释了为什么物体在受到外力作用时会加速。它还解释了为什么物体的质量越大，所需的力越大，加速度越小。

牛顿第三定律也被称为作用与反作用定律，它表明对于每一个作用力，都有一个与之大小相等、方向相反的反作用力。如果物体A对物体B施加一个力，那么物体B对物体A也会施加一个大小相等、方向相反的力。

当我们使用锤子敲击钉子时，我们施加了一个向下的力，钉子对锤子也施加了一个向上的力。这个力使得锤子停止下降。当我们在地面上行走时，我们对地面施加了一个向后的力，地面对我们也施加了一个向前的力。这个力使得我们向前移动。

3.1. 力

力是一个矢量，它有大小和方向。

如果拉动弹簧，弹簧就会拉伸；如果用力拉小车，小车就会移动；如果踢足球，足球就会短暂变形然后飞出去。这些都是接触力（Contact force）的例子。

重力（Gravitational force）是地球对物体的吸引力。它的大小等于物体的质量乘以重力加速度（在地球表面约为9.8 m/s²）。重力总是朝下。

摩擦力（Frictional force）是阻止物体在表面上滑动的力。摩擦力的方向总是与物体相对于表面的运动方向相反。

电磁力（Electromagnetic force）是电荷之间的相互作用力。

3.2. 运动定律

力的国际单位是牛顿（N）：

1 N=1 kg⋅m/s21\ N = 1\ kg \cdot m/s^2

  • 在美国，磅（lb）是力的单位：1 N=0.225 lb1\ N = 0.225\ lb

3.3. 动摩擦力

摩擦力是一种接触力，源于物体与其环境之间的微观相互作用。空气摩擦力（Air friction）影响着各种交通工具，流体摩擦力（Fluid friction）影响着船只的运动。摩擦力并不单单是阻碍物体运动的力，它还可以使物体运动。

动摩擦力（Force of kinetic friction）是当两个物体在相对运动时、产生出的抵抗这种运动的力。它的方向总是与物体相对运动的方向相反。

fk=μkNf_{\text{k}} = \mu_{k} N

  • NN是作用于物体上的法向力（Normal force），公式为N=mgN = mg
  • μk\mu_{k}是物体和表面之间的动摩擦系数（Coefficient of kinetic friction）

动摩擦力的特点是它与物体的速度无关，只取决于接触表面的性质和正压力的大小。这就是为什么在相同表面下，重的物体比轻的物体更难推动。

3.4. 静摩擦力

静摩擦力（Static friction forces）是当两个物体试图滑动但实际上并未滑动时、产生的抵抗滑动的力。

0≤fs≤fs, max≤μsN0 \leq f_{\text{s}} \leq f_{\text{s, max}} \leq \mu_{s} N

  • NN是法向力
  • μs\mu_{s}是物体与表面之间最大的静摩擦系数
  • 该公式仅用于计算最大静摩擦力

3.5. 张力

将绳索固定在物体上并拉动它，即可产生张力（Tension force）。张力是绳索内部的拉力，它总是朝着绳索的两端方向。

4. 能量

能量（Energy）以各种形式存在于宇宙中，即使是日常物质中的惰性物质也蕴含着大量的能量。虽然能量可以从一种转化为另一种，但迄今为止的所有观测和实验都表明，宇宙中的能量总量从未发生过变化。

对于孤立系统来说也是如此，孤立系统是一组物体的集合，它们可以相互交换能量，但不能与宇宙的其他部分交换能量。如果孤立系统中的一种能量形式减少，那么系统中的另一种能量形式必然增加。

例如，如果系统由连接到电池的电机组成，那么电池将化学能转化为电能，电机将电能转化为机械能。了解能量如何从一种形式转化为另一种形式，对所有科学都至关重要。

4.1. 功

功（Work）用于描述力在物体上所做的影响。在物理学中，功是通过力使物体移动一定距离所做的工作。如果力的方向与物体移动的方向一致，那么功就是力和距离的乘积。

功的直观定义：

W=F⋅dW = F \cdot d

  • FF是作用在物体上的力的大小
  • dd是物体位移的大小
  • 这个定义仅给出了当力恒定，并且位移平行时物体所做的功，这代表着在这个定义下位移必须沿着一条直线

功是一个标量，对比矢量更容易处理。它与方向无关，也不明确取决于时间。因为功的单位是力和距离的单位，所以国际单位是牛顿米（N·m），也称为焦耳（J）。

如果力的方向与物体移动的方向不一致，那么我们可以使用以下公式：

W=F⋅d⋅cos⁡θW = F \cdot d \cdot \cos \theta

  • θ\theta是力和位移之间的夹角

4.2. 动能

动能（Kinetic energy）是物体由于运动而具有的能量。

K=12 mv2K = \frac{1}{2}\ m v^2

功-能定理（Work-energy theorem）表明，当力对物体做功时，物体的动能会增加。这个定理可以用来解释为什么物体在受到外力作用时会加速。

W=ΔKW = \Delta K

  • 该定理是牛顿第二定律的一个推论，为我们提供了一种计算物体速度变化的方法
  • 例如你用力推动一个静止的物体使其开始运动，那么你对物体做的功就等于物体获得的动能。如果你用力使一个正在运动的物体停下来，那么你对物体做的功就等于物体失去的动能

净功（Net work）等同于物体动能的变化：

Wnet=KEf−KEi=ΔKEW_{\text{net}} = KE_f - KE_i = \Delta KE

净功是所有作用在物体上的力所做的功的总和。如果净功为正，那么物体的动能会增加；如果净功为负，那么物体的动能会减少。

4.3. 保守力和非保守力

力可以被分为两种类型：保守力（Conservative force）和非保守力（Non-conservative force）。

保守力的特点是它做的功仅仅取决于物体的初始位置和最终位置，而不依赖于物体从初始位置到最终位置所走的路径。换句话说，对于保守力而言，从一点到另一点的路径无论如何变化，只要初始和最终位置相同，做的功就是相同的。重力和弹簧力便是两个常见的保守力。

保守力的一个重要特性便是它们可以与势能（Potential energy）联系起来。

非保守力也被称为耗散力（Dissipative force），它们做的功取决于物体所走的路径。摩擦力和空气阻力便是两个常见的非保守力。

非保守力通常会导致物体的机械能（Mechanical energy，是动能和势能的和）减少，因为它们会将物体的机械能转化为其他形式的能量，例如热能。

Wnc+Wc=ΔKEW_{\text{nc}} + W_{\text{c}} = \Delta KE

4.4. 重力势能

具有动能的物体可以对另一个物体做功，例如一个正在移动的锤子可以把钉子钉进墙里。高架上的砖块也能做功：它可以从架子上掉下来、加速向下、正中钉子、将钉子打入地板。这块砖可以具有势能，因为从它的位置来看，它有可能做功。

重力是一种保守力，每一种保守力都可以从中找到一种叫做势能函数的特殊表达式。重力功（Gravitational work）是当物体在重力的作用下位移时、重力对物体做的功。

Wg=Fdcos⁡θ=mg(yi−yf)cos⁡0°=−mg(yf−yi)W_g = Fd \cos \theta = mg(y_i-y_f) \cos 0 \degree = -mg(y_f-y_i)

  • 该公式描述了一本质量为mm的书从yiy_i摔落到yfy_f（不考虑空气摩擦力）
  • 计算净功：Wnet=Wnc+Wg=ΔKEW_{\text{net}} = W_{nc} + W_g = \Delta KE
    • WncW_{nc}意味着由非保守力做的功

重力势能（Gravitational potential energy）是一个物体由于其在地球表面或其他天体表面以上的位置而获得的能量。

PE=mgyPE = mgy

  • yy是相对于地球表面、物体所在的高度

重力功和重力势能的关系：

Wg=−(PEf−PEi)=−(mgyf−mgyi)W_g = - (PE_f-PE_i) = - (mgy_f - mgy_i)

根据这两个公式，功-能定理（对于非保守力）的公式可以进行扩展：

Wnc=(KEf−KEi)+(PEf−PEi)W_{nc} = (KE_f - KE_i) + (PE_f - PE_i)

4.5. 重力与机械能守恒定律

机械能（Mechanical energy）是一个物体的动能和势能之和。假设在一个封闭的系统中，如果只有保守力作用，那么这个物体的机械能就是守恒的。

KEi+PEi=KEf+PEfKE_i + PE_i = KE_f + PE_f

如果重力是系统中唯一做功的力，那么机械能守恒原理的形式为：

12 mvi2+mgyi=12 mvf2+mgyf\frac{1}{2}\ mv^2_i + mgy_i = \frac{1}{2}\ mv^2_f + mgy_f

4.6. 弹簧势能

在拉伸或压缩弹簧时，外力所做的功可以通过消除外力来恢复，因此弹簧力和重力一样、也是保守力。

PEs=12 kx2PE_s = \frac{1}{2}\ kx^2

  • kk是弹簧的硬度
  • xx是弹簧被压缩或拉伸的长度

加上弹簧势能，功-能定理又可以进行一波扩展：

Wnc=(KEf−KEi)+(PEgf−PEgi)+(PEsf−PEsi)W_{nc} = (KE_f - KE_i) + (PE_{gf} - PE_{gi}) + (PE_{sf} - PE_{si})

4.7. 能量守恒定律

能量守恒定律（Conservation of energy）是物理学中的基本定律之一，它指出，在一个封闭的系统中，能量不能被创建也不能被销毁，只能从一种形式转化为另一种形式。也就是说，系统的总能量在任何时候都保持不变。

4.8. 功率

在物理学中，功率（Power）是做功或转移能量的速率。也就是说，功率描述了单位时间内做多少功或转移多少能量。功率的定义式为：

Pˉ=WΔt=FΔxΔt=Fvˉ\bar{P} = \frac{W}{\Delta t} = \frac{F \Delta x}{\Delta t} = F \bar{v}

  • WW是做的功或者转移的能量（瓦特）
  • Δt\Delta t是时间周期

以上是速度平均的情况下，如果是瞬时速度：

P=FvP = Fv

功率的国际单位是焦耳，也可以被称为瓦特：

1 W=1 J/s=1 kg⋅m2/s31\ \text{W} = 1\ \text{J/s} = 1\ \text{kg} \cdot \text{m}^2 / \text{s}^3

单位马力（Horsepower）有时也会被使用：

1 hp=550 ft⋅lbs=746 W1\ \text{hp} = 550\ \frac{\text{ft} \cdot \text{lb}}{\text{s}} = 746\ \text{W}

在发电领域，人们习惯用千瓦时来衡量能量：

1 kWh=(103 W)(3600 s)=(103 J/s)(3600 s)=3.60⋅106J1\ \text{kWh} = (10^3\ \text{W}) (3600\ \text{s}) = (10^3\ \text{J} / \text{s}) (3600\ \text{s}) = 3.60 \cdot 10^6 \text{J}

5. 旋转运动和万有引力

5.1. 角的单位

在物理学中，角度通常用弧度（Radian）来表示。弧度是一个角度单位，它定义为半径等于圆弧长度的角度。弧度的符号是rad。

但在日常生活中，我们通常使用度（Degree）来表示角度。一个圆有360度，一个弧度等于180/π度。

rad=degree⋅π180\text{rad} = \text{degree} \cdot \frac{\pi}{180}

转数（Revolutions）是一个物体绕一个轴旋转的次数，通常用符号rev表示。一个完整的旋转是360度或2π2\pi弧度。

rev=rad⋅12π\text{rev} = \text{rad} \cdot \frac{1}{2\pi}

rpm（Revolutions per minute）是一个物体每分钟绕轴旋转的次数。它是一个常用的单位，特别是在描述发动机和电机的转速时。

已知1转等于2π2\pi弧度，1分钟等于60秒，我们可以得到：

rad/s=rpm⋅2π60\text{rad/s} = \text{rpm} \cdot \frac{2\pi}{60}

5.2. 角速度/加速度

角速度（Angular velocity）是一个物体绕轴旋转的速度。它是角度的变化率，通常用符号ω\omega表示。角速度的国际单位是弧度每秒（rad/s）。

ω=vr\omega = \frac{v}{r}

  • vv是物体的线速度
  • rr是物体绕轴旋转的半径

角加速度（Angular acceleration）是角速度随时间的变化率，通常用符号α\alpha表示。角加速度的国际单位是弧度每秒的平方（rad/s²）。

α=ωt\alpha = \frac{\omega}{t}

以该公式为基底，我们也能推导出：

  • ω=αt\omega = \alpha t
  • t=ωαt = \frac{\omega}{\alpha}

我们也知道角位移θ\theta的公式：θ=12αt2\theta = \frac{1}{2} \alpha t^2，

因此，θ=12α(ωα)2=ω22α\theta = \frac{1}{2} \alpha (\frac{\omega}{\alpha})^2 = \frac{\omega^2}{2\alpha}。

线位移ss的公式为：s=rθs = r \theta，所以s=rω22αs = r \frac{\omega^2}{2\alpha}。

而线性速度和角速度之间的关系是：

v=rωv = r \omega

线性加速度和角加速度之间的关系是：

a=rαa = r \alpha